
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于点
相交于点![]() 和点
和点![]() 两点.
两点.
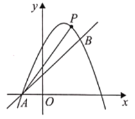
(1)求抛物线的函数表达式;
(2)若点![]() 是位于直线
是位于直线![]() 上方抛物线上的一动点,当
上方抛物线上的一动点,当![]() 的面积
的面积![]() 最大时,求此时
最大时,求此时![]() 的面积
的面积![]() 及点
及点![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是等腰三角形?若存在,直接写出
是等腰三角形?若存在,直接写出![]() 点的坐标(不用说理);若不存在,请说明理由.
点的坐标(不用说理);若不存在,请说明理由.
【答案】(1)所求抛物线的函数表达式为![]() ;(2)
;(2)![]() 的面积
的面积![]() 有最大值是
有最大值是![]() ,此时点
,此时点![]() 坐标为
坐标为![]() ;(3)存在点
;(3)存在点![]() 坐标为
坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先根据点B在直线y=x+1求出其坐标,再将A,B坐标代入抛物线解析式求解可得;
(2)作PM⊥x轴于点M,交AB于点N,设点P的坐标为(m,-m2+2m+3),点N的坐标为(m,m+1),依据S△PAB=S△PAN+S△PBN列出函数解析式,利用二次函数的性质求解可得;
(3)设点Q坐标为(n,0),结合各点坐标得出QA2=(-1-n)2,QB2=(2-n)2+9,AB2=18,再根据等腰三角形的定义分三种情况分别求解可得.
解(1)![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]() ,
,
![]() 点
点![]() 坐标为
坐标为![]() ,
,
![]() 点
点![]() 和点
和点![]() 在抛物线
在抛物线![]() 上,
上,
![]() ,
,
解得![]() ,
,
![]() 所求抛物线的函数表达式为
所求抛物线的函数表达式为![]() ;
;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,
,
设点![]() 的横坐标为
的横坐标为![]() ,
,
则点![]() 的坐标为
的坐标为![]() ,
,
点![]() 的坐标为
的坐标为![]() ,
,
![]() 点
点![]() 是位于直线
是位于直线![]() 上方,
上方,
![]()
![]()
![]() .
.
![]() 的面积
的面积![]()
![]()

![]() ,
,![]()
![]() 抛物线开口向下,又
抛物线开口向下,又![]() ,
,
![]() 当
当![]() 时,
时,
![]() 的面积
的面积![]() 有最大值,
有最大值,
最大值是![]() .
.
此时点![]() 坐标为
坐标为![]() ;
;
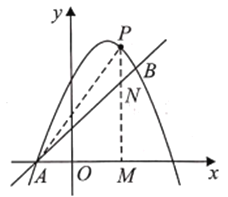
(3)存在点![]() 坐标为
坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
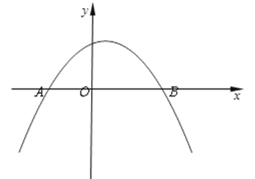
【题目】如图,已知平面直角坐标系![]() ,抛物线
,抛物线![]() 与
与![]() 轴交于点A(-2,0)和点B(4,0) .
轴交于点A(-2,0)和点B(4,0) .
(1)求这条抛物线的表达式和对称轴;
(2)点C在线段OB上,过点C作CD⊥![]() 轴,垂足为点C,交抛物线与点D,E是BD中点,联结CE并延长,与
轴,垂足为点C,交抛物线与点D,E是BD中点,联结CE并延长,与![]() 轴交于点F.
轴交于点F.
①当D恰好是抛物线的顶点时,求点F的坐标;
②联结BF,当△DBC的面积是△BCF面积的![]() 时,求点C的坐标.
时,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
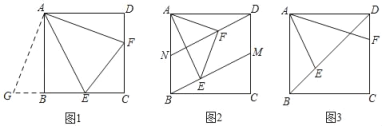
【题目】已知:正方形ABCD,∠EAF=45°.
(1)如图,当点E、F分别在边BC、CD上,连接EF,求证:EF=BE+DF;
童威同学是这样思考的,请你和他一起完成如下解答:证明:将△ADF绕点A顺时针旋转90°,得△ABG,所以△ADF≌△ABG.
(2)如图,点M、N分别在边AB、CD上,且BN=DM.当点E、F分别在BM、DN上,连接EF,探究三条线段EF、BE、DF之间满足的数量关系,并证明你的结论.
(3)如图,当点E、F分别在对角线BD、边CD上.若FC=2,则BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知二次函数y=ax2﹣2ax﹣3a(a>0)图象与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,顶点为D.
(1)求点A,B的坐标;
(2)若M为对称轴与x轴交点,且DM=2AM.
①求二次函数解析式;
②当t﹣2≤x≤t时,二次函数有最大值5,求t值;
③若直线x=4与此抛物线交于点E,将抛物线在C,E之间的部分记为图象记为图象P(含C,E两点),将图象P沿直线x=4翻折,得到图象Q,又过点(10,﹣4)的直线y=kx+b与图象P,图象Q都相交,且只有两个交点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
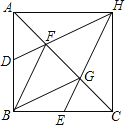
【题目】已知:如图,在△ABC中,AB=BC,∠ABC=90°,点D、E分别是边AB、BC的中点,点F、G是边AC的三等分点,DF、EG的延长线相交于点H,连接HA、HC.
(1)求证:四边形FBGH是菱形;
(2)求证:四边形ABCH是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在△ABC内,点P、Q、R分别在边AB、BC、CA上,且OP∥BC,OQ∥CA,OR∥AB,OP=OQ=OR=x,BC=a,CA=b,AB=c,则x=( )
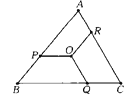
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com