练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

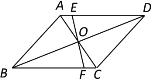
    【题目】如图，平行四边形的对角线、交于点，过点的线段与、分别交于点、，如果，，，那么四边形的周长为__．

    【答案】12

    【解析】

    根据平行四边形的性质知，AB=CD=4，AD=BC=5，AO=OC，∠OAD=∠OCF，∠AOE和∠COF是对顶角相等，根据全等三角形的性质得到OF=OE=，CF=AE，于是可得到结论．

    ∵四边形ABCD是平行四边形，
    ∴AB=CD=4，AD=BC=5，AO=OC，∠OAD=∠OCF，∠AOE=∠COF，
    ∴△OAE≌△OCF（AAS），
    ∴OF=OE=，CF=AE，
    ∴四边形EFCD的周长=ED+CD+CF+OF+OE
    =ED+AE+CD+OE+OF
    =AD+CD+OE+OF
    =4+5++
    =12．
    故答案为：12．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y＝－x 2＋bx＋c与x轴交于A、B两点，与y轴交于点C，已知经过B、C两点的直线的表达式为y＝－x＋3．

    (1)求抛物线的函数表达式；

    (2)点P(m，0)是线段OB上的一个动点，过点P作y轴的平行线，交直线BC于D，交抛物线于E，EF∥x轴，交直线BC于F，DG∥x轴，FG∥y轴，DG与FG交于点G．设四边形DEFG的面积为S，当m为何值时S最大，最大值是多少？

    (3)在坐标平面内是否存在点Q，将△OAC绕点Q逆时针旋转90°，使得旋转后的三角形恰好有两个顶点落在抛物线上．若存在，求出所有符合条件的点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一批货物准备运往某地，有甲、乙、丙三辆卡车可雇用.已知甲、乙、丙三辆车每次运货量不变，且甲、乙两车单独运完这批货物分别用次；甲、丙两车合运相同次数，运完这批货物，甲车共运吨；乙、丙两车合运相同次数，运完这批货物乙车共运吨，现甲、乙、丙合运相同次数把这批货物运完，货主应付甲车主的运费为___________ 元.(按每吨运费元计算)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解全区5000名初中毕业生的体重情况，随机抽测了200名学生的体重，频率分布如图所示（每小组数据可含最小值，不含最大值），其中从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05，由此可估计全区初中毕业生的体重不小于60千克的学生人数约为___人.

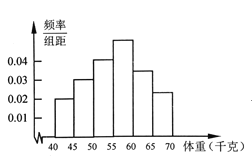
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解全区5000名初中毕业生的体重情况，随机抽测了200名学生的体重，频率分布如图所示（每小组数据可含最小值，不含最大值），其中从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05，由此可估计全区初中毕业生的体重不小于60千克的学生人数约为___人.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

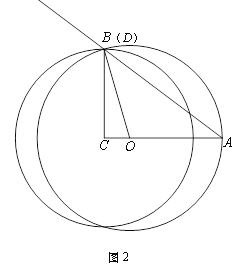
    【题目】如图，在Rt△ABC中，，，，点是边上一个动点（不与、重合），以点为圆心，为半径作，与射线交于点；以点为圆心，为半径作，设．

    （1）如图，当点与点重合时，求的值；

    （2）当点在线段上，如果与的另一个交点在线段上时，设，试求与之间的函数解析式，并写出的取值范围；

    （3）在点的运动的过程中，如果与线段只有一个公共点，请直接写出的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，禁止捕鱼期间，某海上稽查队在某海域巡逻，上午某一时刻在A处接到指挥部通知，在他们东北方向距离12海里的B处有一艘捕鱼船，正在沿南偏东75°方向以每小时10海里的速度航行，稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发，在C处成功拦截捕鱼船，则巡逻船从出发到成功拦截捕鱼船所用的时间是（　　）

    A. 1小时 B. 2小时 C. 3小时 D. 4小时

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y＝﹣x2+bx+c与一直线相交于A（1，0）、C（﹣2，3）两点，与y轴交于点N，其顶点为D．

    （1）求抛物线及直线AC的函数关系式；

    （2）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值及此时点P的坐标；

    （3）在对称轴上是否存在一点M，使△ANM的周长最小．若存在，请求出M点的坐标和△ANM周长的最小值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点A是双曲线 （k1＞0）上一点，点A的横坐标为1，过点A作平行于y轴的直线，与x轴交于点B，与双曲线（k2＜0）交于点C．点D（m，0）是x轴上一点，且位于直线AC右侧，E是AD的中点．

    （1）当m＝4时，求△ACD的面积（用含k1、k2的代数式表示）；

    （2）若点E恰好在双曲线（k1＞0）上，求m的值；

    （3）设线段EB的延长线与y轴的负半轴交于点F，当点D的坐标为D（2，0）时，若△BDF的面积为1，且CF∥AD，求k1的值，并直接写出线段CF的长．

    查看答案和解析>>

    同步练习册答案