
【题目】如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:
①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=![]() MF.其中正确结论的是( )
MF.其中正确结论的是( )

A. ①③④ B. ②④⑤ C. ①③④⑤ D. ①③⑤
【答案】C
【解析】
根据正方形的性质可得AB=BC=AD,∠ABC=∠BAD=90°,再根据中点定义求出AE=BF,然后利用“边角边”证明△ABF和△DAE全等,根据全等三角形对应角相等可得∠BAF=∠ADE,然后求出∠ADE+∠DAF=∠BAD=90°,从而求出∠AMD=90°,再根据邻补角的定义可得∠AME=90°,得出①正确;
根据中线的定义判断出∠ADE≠∠EDB,然后求出∠BAF≠∠EDB,判断出②错误;
根据直角三角形的性质判断出△AED、△MAD、△MEA三个三角形相似,利用相似三角形对应边成比例可得![]() =2,然后求出MD=2AM=4EM,判断出④正确,设正方形ABCD的边长为2a,利用勾股定理列式求出AF,再根据相似三角形对应边成比例求出AM,然后求出MF,消掉a即可得到AM=
=2,然后求出MD=2AM=4EM,判断出④正确,设正方形ABCD的边长为2a,利用勾股定理列式求出AF,再根据相似三角形对应边成比例求出AM,然后求出MF,消掉a即可得到AM=![]() MF,判断出③正确.
MF,判断出③正确.
在正方形ABCD中,AB=BC=AD,∠ABC=∠BAD=90°,
∵E、F分别为边AB,BC的中点,
∴AE=BF=![]() BC,
BC,
在△ABF和△DAE中,
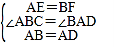 ,
,
∴△ABF≌△DAE(SAS),
∴∠BAF=∠ADE,
∵∠BAF+∠DAF=∠BAD=90°,
∴∠ADE+∠DAF=∠BAD=90°,
∴∠AMD=180°﹣(∠ADE+∠DAF)=180°﹣90°=90°,
∴∠AME=180°﹣∠AMD=180°﹣90°=90°,故①正确;
∵DE是△ABD的中线,
∴∠ADE≠∠EDB,
∴∠BAF≠∠EDB,故②错误;
∵∠BAD=90°,AM⊥DE,
∴△AED∽△MAD∽△MEA,
∴![]() =2,
=2,
∴AM=2EM,MD=2AM,
∴MD=2AM=4EM,故④正确;
设正方形ABCD的边长为2a,则BF=a,
在Rt△ABF中,AF=![]() ,
,
∵∠BAF=∠MAE,∠ABC=∠AME=90°,
∴△AME∽△ABF,
∴![]() ,
,
即![]() ,
,
解得AM=![]() ,
,
∴MF=AF﹣AM=![]() a﹣
a﹣![]() =
=![]() ,
,
∴AM=![]() MF,故⑤正确;
MF,故⑤正确;
如图,过点M作MN⊥AB于N,
则![]() ,
,
即![]() ,
,
解得MN=![]() a,AN=
a,AN=![]() a,
a,
∴NB=AB﹣AN=2a﹣![]() a=
a=![]() a,
a,
根据勾股定理,BM=![]() ,
,
过点M作GH∥AB,过点O作OK⊥GH于K,
则OK=a﹣![]() a=
a=![]() a,MK=
a,MK=![]() a﹣a=
a﹣a=![]() a,
a,
在Rt△MKO中,MO=![]() ,
,
根据正方形的性质,BO=2a×![]() =
=![]() a,
a,
∵BM2+MO2=( ![]() a)2+(
a)2+(![]() a)2=2a2,
a)2=2a2,
BO2=(![]() a)2=2a2,
a)2=2a2,
∴BM2+MO2=BO2,
∴△BMO是直角三角形,∠BMO=90°,故③正确;
综上所述,正确的结论有①③④⑤共4个.

故选:C.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,AO平分∠BAC,AO⊥BC,DE⊥BC,GH⊥BC,垂足分别为O、E、H,且DO∥AC,∠B=43°,则图中角的度数为47°的角的个数是( )

A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”,比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式为两人对抗赛,即把四种比赛项目写在4张完全相同的卡片上,比赛时,比赛的两人从中随机抽取1张卡片作为自己的比赛项目(不放回,且每人只能抽取一次)比赛时,小红和小明分到一组.(1)小明先抽取,那么小明抽到唐诗的概率是多少?
(2)小红擅长唐诗,小红想:“小明先抽取,我后抽取”抽到唐诗的概率是不同的,且小明抽到唐诗的概率更大,若小红后抽取,小红抽中唐诗的概率是多少?小红的想法对吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB和△APQ都是等边三角形.
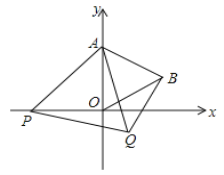

⑴求点B的坐标;
⑵试判断直线AB与直线BQ的位置关系,并证明;
⑶连接OQ,当OQ∥AB时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2分别是7×6的网格,网格中的每个小正方形的边长均为1,点A、B在小正方形的顶点上.
(1)在图1中确定点C(点C在小正方形的顶点上),画出三角形ABC,使tanB=1,△ABC的面积为10;
(2)在图2中确定点D(点D在小正方形的顶点上),画出三角形ABD,使△ABD是以AB为斜边的直角三角形,且AD>BD,直接写出∠DAB的余弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班全体学生2018年初中毕业体育考试的成绩统计如表
成绩(分) | 85 | 89 | 92 | 94 | 95 | 98 | 99 |
人数(人) | 2 | 5 | 6 | 6 | 8 | 6 | 7 |
根据表中的信息判断,下列结论中错误的是( )
A. 该班一共有40名同学
B. 该班学生这次考试成绩的众数是95分
C. 该班学生这次考试成绩的中位数是95分
D. 该班学生这次考试成绩的平均数是95
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们曾学过定理“在直角三角形中,如果一个锐角等于![]() ,那么它所对的直角边等于斜边的一半”,其逆命题也是成立的,即“在直角三角形中,如果一直角边等于斜边的一半,那么该直角边所对的角为
,那么它所对的直角边等于斜边的一半”,其逆命题也是成立的,即“在直角三角形中,如果一直角边等于斜边的一半,那么该直角边所对的角为![]() ”.如图,在
”.如图,在![]() 中,
中,![]() ,如果
,如果![]() ,那么
,那么![]() .
.
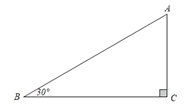
请你根据上述命题,解决下面的问题:

(1)如图1,![]() ,
,![]() 为格点,以
为格点,以![]() 为圆心,
为圆心,![]() 长为半径画弧交直线
长为半径画弧交直线![]() 于点
于点![]() ,则
,则![]() ______
______![]() ;
;
(2)如图2,![]() 、
、![]() 为格点,按要求在网格中作图(保留作图痕迹)。
为格点,按要求在网格中作图(保留作图痕迹)。
作![]() ,使点
,使点![]() 在直线
在直线![]() 上,并且
上,并且![]() ,
,![]() .
.
(3)如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 内一点,
内一点,![]() ,
,![]() 于
于![]() ,且
,且![]() .
.
①求![]() 的度数;
的度数;
②求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=2AB,BD为∠ABC的角平分线,∠ADB=45°,过点A作AE⊥BD于点E,若BE=![]() ,则DE的长为__________
,则DE的长为__________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com