
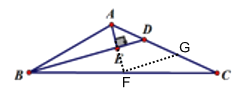
【题目】如图,在△ABC中,BC=2AB,BD为∠ABC的角平分线,∠ADB=45°,过点A作AE⊥BD于点E,若BE=![]() ,则DE的长为__________
,则DE的长为__________

【答案】![]()
【解析】
延长AE交BC于F,过点F作FG∥BD交AC于G,利用ASA易证△ABE≌△FBE,可得AE=EF,AB=BF,进而得到FG是△BDC的中位线,DE是△AFG的中位线,然后根据中位线的性质列方程求解即可.
解:如图,延长AE交BC于F,过点F作FG∥BD交AC于G,
∵BD为∠ABC的角平分线,AE⊥BD,
∴∠ABE=∠FBE,∠AEB=∠FEB=90°,
又∵BE=BE,
∴△ABE≌△FBE(ASA),
∴AE=EF,AB=BF,
∴BC=2AB=2BF,E为AF中点,
∴F为BC中点,
∵FG∥BD,
∴FG是△BDC的中位线,DE是△AFG的中位线,
∴FG=2DE,FG=![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:
①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=![]() MF.其中正确结论的是( )
MF.其中正确结论的是( )

A. ①③④ B. ②④⑤ C. ①③④⑤ D. ①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(3,4)、B(1,1)、C(4,2).
(1)画出△ABC绕点B逆时针旋转90°后得到的△A1BC1,其中A、C分别和A1、C1对应.
(2)平移△ABC,使得A点落在x轴上,B点落在y轴上,画出平移后的△A2B2C2,其中A、B、C分别和A2B2C2对应.
(3)填空:在(2)的条件下,设△ABC,△A2B2C2的外接圆的圆心分别为M、M2,则MM2= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明调查了班级里20位同学本学期购买课外书的花费情况,并将结果绘制成了如图的统计图.在这20位同学中,本学期购买课外书的花费的众数和中位数分别是( )

A. 50,50 B. 50,30 C. 80,50 D. 30,50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在山坡坡脚C处测得一座建筑物顶点A的仰角为63.4°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为53°.已知BC=90米,且B、C、D在同一条直线上,山坡坡度i=5:12.
(1)求此人所在位置点P的铅直高度.(结果精确到0.1米)
(2)求此人从所在位置点P走到建筑物底部B点的路程(结果精确到0.1米)
(测倾器的高度忽略不计,参考数据:tan53°≈![]() ,tan63.5°≈2)
,tan63.5°≈2)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线![]() 上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2019的坐标是_________________.
上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2019的坐标是_________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用无刻度的直尺绘图.
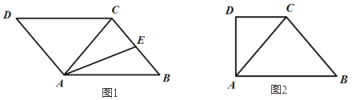
(1)如图1,在![]() 中,AC为对角线,AC=BC,AE是△ABC的中线.画出△ABC的高CH
中,AC为对角线,AC=BC,AE是△ABC的中线.画出△ABC的高CH
(2)如图2,在直角梯形![]() 中,
中,![]() ,AC为对角线,AC=BC,画出△ABC的高CH.
,AC为对角线,AC=BC,画出△ABC的高CH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线l:y=![]() x+m交x轴于点A,二次函数y=ax2﹣3ax+c(a≠0,且a、c是常数)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,与直线l交于点D,已知CD与x轴平行,且S△ACD:S△ABD=3:5.
x+m交x轴于点A,二次函数y=ax2﹣3ax+c(a≠0,且a、c是常数)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,与直线l交于点D,已知CD与x轴平行,且S△ACD:S△ABD=3:5.
(1)求点A的坐标;
(2)求此二次函数的解析式;
(3)点P为直线l上一动点,将线段AC绕点P顺时针旋转α°(0°<α°<360°)得到线段A'C'(点A,A'是对应点,点C,C'是对应点).请问:是否存在这样的点P,使得旋转后点A'和点C'分别落在直线l和抛物线y=ax2﹣3ax+c的图象上?若存在,请直接写出点A'的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com