
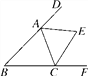
【题目】如图,∠B=46°,△ABC的外角∠DAC和∠ACF的平分线交于点E,则∠AEC的度数为________.
【答案】67°
【解析】根据三角形内角和定理、角平分线的定义以及三角形外角定理求得:
![]() ∠DAC+
∠DAC+![]() ∠ACF=
∠ACF=![]() (∠B+∠B+∠1+∠2)=113°;最后在△AEC中利用三角形内角和定理可以求得∠AEC的度数.
(∠B+∠B+∠1+∠2)=113°;最后在△AEC中利用三角形内角和定理可以求得∠AEC的度数.
如图:
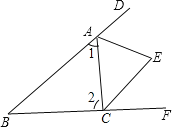
∵三角形的外角∠DAC和∠ACF的平分线交于点E,
∴∠EAC=![]() ∠DAC,∠ECA=
∠DAC,∠ECA=![]() ∠ACF,
∠ACF,
∵∠DAC=∠B+∠2,∠ACF=∠B+∠1.
∴![]() ∠DAC+
∠DAC+![]() ∠ACF=
∠ACF=![]() (∠B+∠2)+
(∠B+∠2)+![]() (∠B+∠1)=
(∠B+∠1)=![]() (∠B+∠B+∠1+∠2),
(∠B+∠B+∠1+∠2),
∵∠B=46°(已知),∠B+∠1+∠2=180°(三角形内角和定理),
∴![]() ∠DAC+
∠DAC+![]() ∠ACF=113°.
∠ACF=113°.
∴∠AEC=180°(![]() ∠DAC+
∠DAC+![]() ∠ACF)=67°.
∠ACF)=67°.
故答案是:67°.


 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价20元,乒乓球每盒定价5元.现两家商店搞促销活动,甲店的优惠办法是:每买一副乒乓球拍赠一盒乒乓球;乙店的优惠办法是:全部商品按定价的9折出售.某班需购买乒乓球拍4副,乒乓球若干盒(不少于4盒).

(1)当购买乒乓球的盒数为x盒时,在甲店购买需付款 元?在乙店 购买需付款 元?(用含x的代数式表示)
(2)当购买乒乓球盒数为10盒时,去哪家商店购买较合算?请计算说明.
(3) 当购买乒乓球盒数为10盒时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并求出此时需付多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区的电力资源丰富,并且得到了较好的开发.该地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的函数图像如图所示.
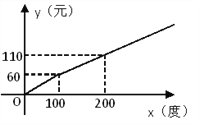
(1)月用电量为100度时,应交电费 元;
(2)当x≥100时,求y与x之间的函数关系式;
(3)月用电量为260度时,应交电费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】具备下列条件的三角形ABC中,不为直角三角形的是( )
A.∠A+∠B=∠C B.∠A=∠B=![]() ∠C
∠C
C.∠A=90°﹣∠B D.∠A﹣∠B=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个自然数的立方,可以分裂成若干个连续奇数的和。例如:![]() 和
和![]() 分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即
分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即![]() =3+5;
=3+5;![]() =7+9+11;
=7+9+11;![]() =13+15+17+19;…;若
=13+15+17+19;…;若![]() 也按照此规律来进行“分裂”,则
也按照此规律来进行“分裂”,则![]() “分裂”出的奇数中,最大的奇数是______.
“分裂”出的奇数中,最大的奇数是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于圆O,点E在对角线AC上. 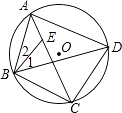
(1)若BC=DC,∠CBD=39°,求∠BCD的度数;
(2)若在AC上有一点E,且EC=BC=DC,求证:∠1=∠2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克) |
|
|
|
|
|
|
筐 数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最轻的一筐重______千克;
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价![]() 元,则出售这20筐白菜可卖多少元?
元,则出售这20筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在RtABC中,∠ACB=90°,BAC=30°,BC=6. (I)如图①,将线段CA绕点C顺时针旋转30°,所得到与AB交于点M,则CM的长=;
(II)如图②,点D是边AC上一点D且AD=2 ![]() ,将线段AD绕点A旋转,得线段AD′,点F始终为BD′的中点,则将线段AD绕点A逆时针旋转度时,线段CF的长最大,最大值为 .
,将线段AD绕点A旋转,得线段AD′,点F始终为BD′的中点,则将线段AD绕点A逆时针旋转度时,线段CF的长最大,最大值为 . 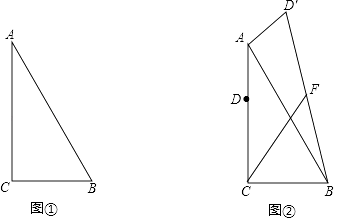
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com