【题目】一个自然数的立方，可以分裂成若干个连续奇数的和。例如：
和
分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和，即
=3+5；
=7+9+11； =13+15+17+19；…；若
也按照此规律来进行“分裂”，则“分裂”出的奇数中，最大的奇数是______.
科目：初中数学 来源： 题型：
【题目】(1)方法回顾：在学习三角形中位线时，为了探索三角形中位线的性质，思路如下：
第一步添加辅助线：如图1，在
中，延长
（分别是
的中点）到点
，使得
，连接
；
第二步证明
，再证四边形
是平行四边形，从而得出三角形中位线的性质结论：____________________________________（请用DE与BC表示）
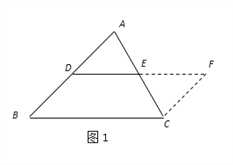
（2）问题解决：如图2，在正方形ABCD中，E为AD的中点，G、F分别为AB、CD边上的点，若AG＝2，DF＝3，∠GEF＝90°，求GF的长．
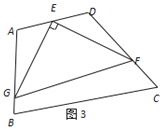
（3）拓展研究：如图3，在四边形ABCD中，∠A＝105°，∠D＝120°，E为AD的中点，G、F分别为AB、CD边上的点，若AG＝
，DF＝2，∠GEF＝90°，求GF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知数轴上三点M，O，N对应的数分别为－1，0，3，点P为数轴上任意一点，其对应的数为x．
（1）MN的长为 ；
（2）如果点P到点M、点N的距离相等，那么x的值是 ；
（3）数轴上是否存在点P，使点P到点M、点N的距离之和是8？若存在，直接写出x的值；若不存在，请说明理由．
（4）如果点P以每分钟1个单位长度的速度从点O向左运动，同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动．设t分钟时点P到点M、点N的距离相等，求t的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD中，G为BC边上一点，BE⊥AG于E，DF⊥AG于F，连接DE．
（1）求证：△ABE≌△DAF；
（2）若AF=1，S△ADE=8，求EF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图A、B分别为数轴上的两点，A点对应的数为-10，B点对应的数为90．
（1）请写出与A，B两点距离相等的M点对应的数；
（2）现在有一只电子蚂蚁P从B点出发时，以3个单位/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以2个单位/秒的速度向右运动，设两只电子蚂蚁在数轴上的C点相遇，求C点对应的数是多少.
（3）若当电子蚂蚁P从B点出发时，以3个单位/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以2个单位/秒的速度向右运动，求经过多长的时间两只电子蚂蚁在数轴上相距35个单位长度.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校在“数学小论文”评比活动中，共征集到论文100篇，对论文评比的分数（分数为整数）整理后，分组画出频数分布直方图（如图），已知从左到右5个小长方形的高的比为l：3：7：6：3，那么在这次评比中被评为优秀的论文（分数大于或等于80分为优秀）有____篇．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点D、E、F分别在正三角形ABC的三边上，且△DEF也是正三角形，若△ABC的边长为a，△DEF的边长为b．则△AEF的内切圆半径为 ．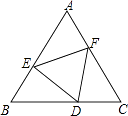 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】a、b、c在数轴上的位置如图所示，则：
（1）用“＜、＞、＝”填空：a____0，b____0，c_____0；
（2）用“＜、＞、＝”填空：﹣a____0，a﹣b____0，c﹣a____0；
（3）化简：|﹣a|﹣|a﹣b|+|c﹣a|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
