
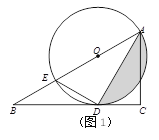
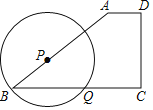
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯCЃН90ЁуЃЌOЮЊаББпABЩЯвЛЕуЃЌвдOЮЊдВаФЁЂOAЮЊАыОЖЕФдВЧЁКУгыBCЯрЧагкЕуDЃЌгыABЕФСэвЛИіНЛЕуЮЊEЃЌСЌНгDEЃЎ
ЃЈ1ЃЉЧыевГіЭМжагыЁїADEЯрЫЦЕФШ§НЧаЮЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєACЃН3ЃЌAEЃН4ЃЌЪдЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЛ
ЃЈ3ЃЉаЁУїдкНтЬтЙ§ГЬжаЫМПМетбљвЛИіЮЪЬтЃКШчЭМжаЕФЁбOЕФдВаФОПОЙЪЧдѕУДШЗЖЈЕФФиЃПЧыФудкШчЭМжаРћгУжБГпКЭдВЙцевЕНЗћКЯЬтвтЕФдВаФOЃЌВЂаДГіФуЕФзїЭМЗНЗЈЃЎ
ЁОД№АИЁП(1)МћНтЮі;(2)![]() ІаЃ
ІаЃ![]() ;(3)МћНтЮі.
;(3)МћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉBCЮЊдВOЕФЧаЯпЃЌСЌНгODЃЌПЩЭЦГіЁЯEAD=ЁЯODA=ЁЯDACЃЌгЩЁЯEDA=ЁЯDCA=90ЁуЃЌПЩЭЦГіЁїAEDЁзЁїADCЃЎ
ЃЈ2ЃЉИљОнЁїAEDЁзЁїADCЃЌПЩЕУГіADЕФГЄЖШЃЌдйИљОнЁїAEDЕФШ§БпБШР§ЙиЯЕЃЌПЩЭЦГіЁЯAOD=120ЃЌдйРћгУЩШаЮУцЛ§МѕШ§НЧаЮЕФУцЛ§МДПЩЕУЕНвѕгАВПЗжУцЛ§ЃЎ
ЃЈ3ЃЉЂйзїЁЯBACЕФНЧЦНЗжЯпНЛBCБпгкЕуDЃЌЂкЙ§ЕуDзїBCЕФДЙЯпНЛABгкЕуOЃЎЃЈзЂЃКЗНЗЈВЛЮЈвЛЃЉ
НтЃКЃЈ1ЃЉЁїACDгыЁїADEЯрЫЦЃЌШчЭМЃЈ1ЃЉЫљЪОЃЌ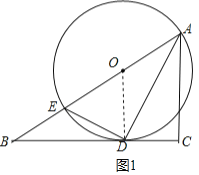
СЌНгODЃЌЁпЁбOЧЁКУгыBCЯрЧагкЕуDЃЌ
ЁрЁЯODB=90ЁуЃЌ
гжЁпЁЯC=90ЁуЃЌ
ЁрODЁЮACЃЌ
ЁрЁЯODA=ЁЯDACЃЌ
ЁпOD=OAЃЌ
ЁрЁЯODA=ЁЯOADЃЌ
ЁрЁЯOAD=ЁЯDACЃЌ
ЁпAEЮЊЁбOЕФжБОЖЃЌ
ЁрЁЯADE=90ЁуЃЌ
ЁрЁЯADE=ЁЯCЃЌ
ЁрЁїACDЁзЁїADEЃЎ
ЃЈ2ЃЉЁпЁїACDЁзЁїADEЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрAD=2![]() ЃЌ
ЃЌ
ЁпAC=3ЃЌИљОнЙДЙЩЖЈРэЕУCD=![]() ЃЌ
ЃЌ
ЁрsinЁЯDAC=![]() ЃЌ
ЃЌ
ЁрЁЯDAC=ЁЯEAD=ЁЯODA=30ЁуЃЌ
ЁрЁЯAOD=120ЁуЃЌ
ЁрSЁїOAD=![]() OA2=
OA2=![]() ЃЌ
ЃЌ
ЁрS=![]() ЃЎ
ЃЎ
ЃЈ3ЃЉШчЭМ2ЫљЪОЃЌзїЭМЗНЗЈЃК
ЂйвдAЮЊдВаФЃЌACГЄЮЊАыОЖЛЛЁЃЌНЛABгкЕуHЃЌвдHЁЂCЮЊдВаФЃЌДѓгк![]() CHГЄЮЊАыОЖЛЛЁЃЌНЛгкЕуGЃЌСЌНгAGЃЌAGМДЮЊЁЯBACЕФНЧЦНЗжЯпЃЌAGгыBCЕФНЛЕуМДЮЊЕуDЃЎ
CHГЄЮЊАыОЖЛЛЁЃЌНЛгкЕуGЃЌСЌНгAGЃЌAGМДЮЊЁЯBACЕФНЧЦНЗжЯпЃЌAGгыBCЕФНЛЕуМДЮЊЕуDЃЎ
ЂквдDЮЊдВаФЃЌDCГЄЮЊАыОЖЛЛЁЃЌНЛBDгкЕуCЁфЃЌвдCЁЂCЁфЮЊдВаФЃЌДѓгк![]() CCЁфЮЊАыОЖЛЛЁЃЌЗжБ№НЛгкЕуEЁЂFЃЌСЌНгEFЃЌEFМДЮЊCCЁфЕФДЙжБЦНЗжЯпЃЌEFгыABЕФНЛЕуМДЮЊЕуOЃЎ
CCЁфЮЊАыОЖЛЛЁЃЌЗжБ№НЛгкЕуEЁЂFЃЌСЌНгEFЃЌEFМДЮЊCCЁфЕФДЙжБЦНЗжЯпЃЌEFгыABЕФНЛЕуМДЮЊЕуOЃЎ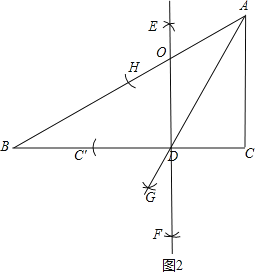



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдкЬнаЮABCDжаЃЌADЁЮBCЃЌAB=BCЃЌDCЁЭBCЃЌЧвAD=1ЃЌDC=3ЃЌЕуPЮЊБпABЩЯвЛЖЏЕуЃЌвдPЮЊдВаФЃЌBPЮЊАыОЖЕФдВНЛБпBCгкЕуQЃЎ
(1)ЧѓABЕФГЄЃЛ
(2)ЕБBQЕФГЄЮЊ![]() ЪБЃЌЧыЭЈЙ§МЦЫуЫЕУїдВPгыжБЯпDCЕФЮЛжУЙиЯЕЃЎ
ЪБЃЌЧыЭЈЙ§МЦЫуЫЕУїдВPгыжБЯпDCЕФЮЛжУЙиЯЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЬсИпВњЦЗЕФИНМгжЕЃЌФГЙЋЫОМЦЛЎНЋбаЗЂЩњВњЕФ1200МўаТВњЦЗНјааОЋМгЙЄКѓдйЭЖЗХЪаГЁЃЎЯжгаМзЁЂввСНИіЙЄГЇЖМОпБИМгЙЄФмСІЃЌЙЋЫОХЩГіЯрЙиШЫдБЗжБ№ЕНетСНИіЙЄГЇСЫНтЧщПіЃЌЛёЕУШчЯТаХЯЂЃК
аХЯЂвЛЃКМзЙЄГЇЕЅЖРМгЙЄЭъГЩетХњВњЦЗБШввЙЄГЇЕЅЖРМгЙЄЭъГЩетХњВњЦЗЖргУ10ЬьЃЛ
аХЯЂЖўЃКввЙЄГЇУПЬьМгЙЄЕФЪ§СПЪЧМзЙЄГЇУПЬьМгЙЄЪ§СПЕФ1.5БЖЃЎ
ИљОнвдЩЯаХЯЂЃЌЧѓМзЁЂввСНИіЙЄГЇУПЬьЗжБ№ФмМгЙЄЖрЩйМўаТВњЦЗЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
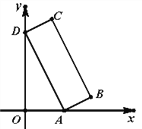
ЁОЬтФПЁПШчЭМЃЌвбжЊОиаЮABCDЕФЖЅЕуAЁЂDЗжБ№ТфдкxжсЁЂyжсЃЌOD=2OA=6ЃЌADЃКAB=3ЃК1ЃЎдђЕуBЕФзјБъЪЧ_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
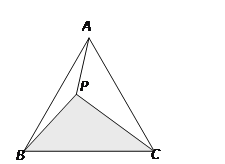
ЁОЬтФПЁПШчЭМЃЌвбжЊPЮЊЕШБпЁїABCаЮФквЛЕуЃЌЧвPAЃН3cmЃЌPBЃН4 cmЃЌPCЃН5 cmЃЌдђЭМжаЁїPBCЕФУцЛ§ЮЊ________cm2ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃЮЊСЫдіЧПбЇЩњЬхжЪЃЌОіЖЈПЊЩшвдЯТЬхг§ПЮЭтЛюЖЏЯюФПЃКAЃКРКЧђ BЃКЦЙХвЧђCЃКг№УЋЧђ DЃКзуЧђЃЌЮЊСЫНтбЇЩњзюЯВЛЖФФвЛжжЛюЖЏЯюФПЃЌЫцЛњГщШЁСЫВПЗжбЇЩњНјааЕїВщЃЌВЂНЋЕїВщНсЙћЛцжЦГЩСЫСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыЛиД№ЯТСаЮЪЬтЃК


ЃЈ1ЃЉетДЮБЛЕїВщЕФбЇЩњЙВгаЁЁ ЁЁШЫЃЛ
ЃЈ2ЃЉЧыФуНЋЬѕаЮЭГМЦЭМЃЈ2ЃЉВЙГфЭъећЃЛ
ЃЈ3ЃЉдкЦНЪБЕФЦЙХвЧђЯюФПбЕСЗжаЃЌМзЁЂввЁЂБћЁЂЖЁЫФШЫБэЯжгХауЃЌЯжОіЖЈДгетЫФУћЭЌбЇжаШЮбЁСНУћВЮМгЦЙХвЧђБШШќЃЌЧѓЧЁКУбЁжаМзЁЂввСНЮЛЭЌбЇЕФИХТЪЃЈгУЪїзДЭМЛђСаБэЗЈНтД№ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
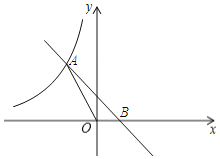
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=-x+1гыЗДБШР§КЏЪ§y=![]() (xЃМ0)ЕФЭМЯѓНЛгкЕуAЃЌгыxжсе§АыжсНЛгкЕуBЃЌЧвSЁїAOB=1ЃЌдђЗДБШР§КЏЪ§НтЮіЪНЮЊ______ЃЎ
(xЃМ0)ЕФЭМЯѓНЛгкЕуAЃЌгыxжсе§АыжсНЛгкЕуBЃЌЧвSЁїAOB=1ЃЌдђЗДБШР§КЏЪ§НтЮіЪНЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌOЪЧЖдНЧЯпACгыBDЕФНЛЕуЃЌMЪЧBCБпЩЯЕФЖЏЕу(ЕуMВЛгыBЁЂCжиКЯ)ЃЌЙ§ЕуCзїCNДЙжБDMНЛABгкЕуNЃЌСЌНсOMЁЂONЁЂMN.ЯТСаЮхИіНсТлЃКЂйЁїCNBЁеЁїDMCЃЛЂк![]() ЃЛЂлONЁЭOMЃЛЂмШєABЃН2ЃЌдђ
ЃЛЂлONЁЭOMЃЛЂмШєABЃН2ЃЌдђ![]() ЕФзюаЁжЕЪЧ1ЃЛЂн
ЕФзюаЁжЕЪЧ1ЃЛЂн![]() .Цфжае§ШЗНсТлЪЧ_________.(жЛЬюЗЌКХ)
.Цфжае§ШЗНсТлЪЧ_________.(жЛЬюЗЌКХ)

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊХзЮяЯпyЃНx2+bx+cЙ§AЃЌBЃЌCШ§ЕуЃЌЕуAЕФзјБъЪЧЃЈ3ЃЌ0ЃЉЃЌЕуCЕФзјБъЪЧЃЈ0ЃЌЉ3ЃЉЃЌЖЏЕуPдкХзЮяЯпЩЯЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЖЏЕуPдкЕкЫФЯѓЯоФкЕФХзЮяЯпЩЯЃЌЙ§ЖЏЕуPзїxжсЕФДЙЯпНЛжБЯпACгкЕуDЃЌНЛxжсгкЕуEЃЌДЙзуЮЊEЃЌЧѓЯпЖЮPDЕФГЄЃЌЕБЯпЖЮPDзюГЄЪБЃЌЧѓГіЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЪЧЗёДцдкЕуPЃЌЪЙЕУЁїACPЪЧвдACЮЊжБНЧБпЕФжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com