
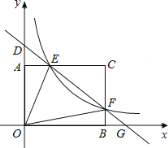
【题目】如图,矩形AOBC的顶点坐标分别为A(0,3),O(0,0),B(4,0),C(4,3),动点F在边BC上(不与B.C重合),过点F的反比例函数y=![]() 的图象与边AC交于点E,直线EF分别与y轴和x轴相交于点D和G.给出下列命题:①若k=4,则△OEF的面积为
的图象与边AC交于点E,直线EF分别与y轴和x轴相交于点D和G.给出下列命题:①若k=4,则△OEF的面积为![]() ;②若k=
;②若k=![]() ,则点C关于直线EF的对称点在x轴上;③满足题设的k的取值范围是0<k≤12;④若DEEG=
,则点C关于直线EF的对称点在x轴上;③满足题设的k的取值范围是0<k≤12;④若DEEG=![]() ,则k=1.其中正确的命题的序号是____________(填序号).
,则k=1.其中正确的命题的序号是____________(填序号).
【答案】②④
【解析】
(1)若k=4,则计算![]() ,故命题①错误;
,故命题①错误;
(2)如答图所示,若k=![]() ,可证明直线EF是线段CN的垂直平分线,故命题②正确;
,可证明直线EF是线段CN的垂直平分线,故命题②正确;
(3)因为点F不经过点C(4,3),所以k≠12,故命题③错误;
(4)求出直线EF的解析式,得到点D、G的坐标,然后求出线段DE、EG的长度;利用算式DEEG=![]() ,求出k=1,故命题④正确.
,求出k=1,故命题④正确.
命题①错误,理由如下:
∵k=4,
∴![]()
∴![]()
∴S△OEF=S矩形AOBCS△AOES△BOFS△CEF
=S矩形AOBC![]() ,
,
![]()
![]()
![]()
∴![]() ,故命题①错误;
,故命题①错误;
命题②正确,理由如下:
∵![]()
∴![]()
∴![]()
如答图,过点E作EM⊥x轴于点M,则EM=3,OM=![]() ;
;
在线段BM上取一点N,使得EN=CE=![]() ,连接NF.
,连接NF.
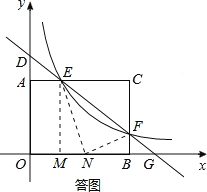
在Rt△EMN中,由勾股定理得:![]()
∴![]()
在Rt△BFN中,由勾股定理得:![]()
∴NF=CF,
又∵EN=CE,
∴直线EF为线段CN的垂直平分线,即点N与点C关于直线EF对称,
故命题②正确;
命题③错误,理由如下:
命题④正确;理由如下:
为简化计算,不妨设k=12m,则E(4m,3),F(4,3m).
设直线EF的解析式为y=ax+b,则有
![]() 解得
解得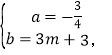
∴![]()
令x=0,得y=3m+3,∴D(0,3m+3);
令y=0,得x=4m+4,∴G(4m+4,0).
如答图,过点E作EM⊥x轴于点M,则OM=AE=4m,EM=3.
在Rt△ADE中,AD=ODOA=3m,AE=4m,由勾股定理得:DE=5m;
在Rt△MEG中,MG=OGOM=(4m+4)4m=4,EM=3,由勾股定理得:EG=5.
∴DEEG=5m×5=25m=![]() ,解得
,解得![]() ,
,
∴k=12m=1,故命题④正确,
综上所述,正确的命题是:②④,
故答案为:②④.


科目:初中数学 来源: 题型:
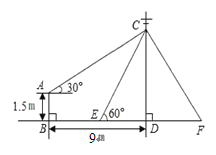
【题目】如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆9m的B处安置高为1.5m的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长.(结果保留根号)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
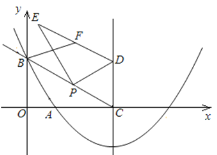
【题目】如图,在平面直角坐标系xOy中,抛物线![]() 过点
过点![]() ,
,![]() ,这条抛物线的对称轴与x轴交于点C,点P为射线CB上一个动点(不与点C重合),点D为此抛物线对称轴上一点,且CPD=
,这条抛物线的对称轴与x轴交于点C,点P为射线CB上一个动点(不与点C重合),点D为此抛物线对称轴上一点,且CPD=![]() .
.
(1)求抛物线的函数表达式;
(2)若点P的横坐标为m,△PCD的面积为S,求S与m之间的函数关系式;
(3)过点P作PE⊥DP,连接DE,F为DE的中点,试求线段BF的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
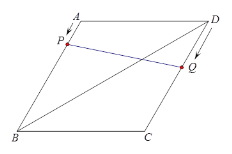
【题目】如图,在菱形ABCD中,已知∠BAD=120°,对角线BD长为12.
(1)求菱形ABCD的周长;
(2)动点P从点A出发,沿A→B的方向,以每秒1个单位的速度向点B运动;在点P出发的同时,动点Q从点D出发,沿D→C→B的方向,以每秒2个单位的速度向点B运动.设运动时间为t(s).
①当PQ恰好被BD平分时,试求t的值;
②连接AQ,试求:在整个运动过程中,当t取怎样的值时,△APQ恰好是一个直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
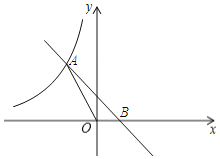
【题目】如图,一次函数y=-x+1与反比例函数y=![]() (x<0)的图象交于点A,与x轴正半轴交于点B,且S△AOB=1,则反比例函数解析式为______.
(x<0)的图象交于点A,与x轴正半轴交于点B,且S△AOB=1,则反比例函数解析式为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某度假村拥有客房40间,该度假村在经营中发现每间客房日租金x(元)与每日租出的客房数(y)有如下关系:
x | 200 | 220 | 260 | 280 |
y | 40 | 35 | 25 | 20 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每日租出的客房数y(间)与每间客房的日租金x(元)之间的关系式.
(2)已知租出的每间客房每日需要清洁费80元,未租出的每间客房每日需要清洁费40元.含x(x≥200)的代数式填表:
租出的客房数 | ______ | 未租出的客房数 | ______ |
租出的每间客房的日收益 | ______ | 所有未租出的客房每日的清洁费 | ______ |
(3)若你是该度假村的老板,你会将每间客房的日租金定为多少元,才能使度假村获得最大日收益?最大日收益是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,以
上,以![]() 为圆心,
为圆心,![]() 为半径的弧经过点
为半径的弧经过点![]() 是弧
是弧![]() 上一个动点.
上一个动点.
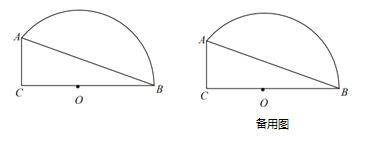
![]() 求半径
求半径![]() 的长;
的长;
![]() 如果点
如果点![]() 是弧
是弧![]() 的中点,联结
的中点,联结![]() ,求
,求![]() 的正切值;
的正切值;
![]() 如果
如果![]() 平分
平分![]() ,延长
,延长![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知梯形ABCD中,AD∥BC,AB=AC,E是边BC上的点,且∠AED=∠CAD,DE交AC于点F.
(1)求证:△ABE∽△DAF;
(2)当ACFC=AEEC时,求证:AD=BE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com