
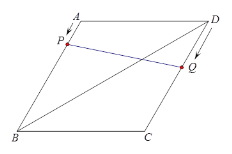
【题目】如图,在菱形ABCD中,已知∠BAD=120°,对角线BD长为12.
(1)求菱形ABCD的周长;
(2)动点P从点A出发,沿A→B的方向,以每秒1个单位的速度向点B运动;在点P出发的同时,动点Q从点D出发,沿D→C→B的方向,以每秒2个单位的速度向点B运动.设运动时间为t(s).
①当PQ恰好被BD平分时,试求t的值;
②连接AQ,试求:在整个运动过程中,当t取怎样的值时,△APQ恰好是一个直角三角形?

【答案】(1)16![]() ;(2) ①
;(2) ①![]() ;②见解析.
;②见解析.
【解析】
(1)连接AC交BD于O,由菱形的性质得出AB=BC=CD=AD,AC⊥BD,∠BCD=∠BAD=120°,∠BCO=![]() ∠BCD=60°,OB=OD=
∠BCD=60°,OB=OD=![]() BD=6,在Rt△BOC中,由三角函数求出BC=4
BD=6,在Rt△BOC中,由三角函数求出BC=4![]() ,即可得出菱形ABCD的周长;
,即可得出菱形ABCD的周长;
(2)①当点Q在CD边上时,设PQ交BD于M,则PM=QM,由平行线求出BP=DQ,根据题意得:AP=t,DQ=2t,则BP=4![]() -t,得出4
-t,得出4![]() -t=2t,解方程即可;
-t=2t,解方程即可;
当点Q在CB边上时,不存在;
②当点Q在CD边上时,若∠PAQ=90°,与平行线的性质得出∠AQD=∠PAQ=90°,则∠DAQ=30°,由直角三角形的性质得出DQ=![]() AD=2
AD=2![]() ,即2t=2
,即2t=2![]() ,求出t的值即可;
,求出t的值即可;
若∠APQ=90°,作AN⊥CD于N,则∠PAN=90°,NQ=AP=t,由直角三角形的性质得出DN=![]() AD=2
AD=2![]() ,得出方程2t=2
,得出方程2t=2![]() +t,解方程即可;
+t,解方程即可;
当点Q在CB边上时,证出∠BPQ=90°,即∠APQ=90°恒成立.得出当2![]() ≤t≤4
≤t≤4![]() 时△APQ都为直角三角形;即可得出答案.
时△APQ都为直角三角形;即可得出答案.
解:(1)连接AC交BD于O,如图1所示:
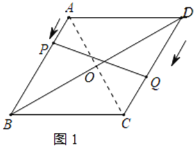
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,∠BCD=∠BAD=120°,∠BCO=![]() ∠BCD=60°,OB=OD=
∠BCD=60°,OB=OD=![]() BD=6,
BD=6,
在Rt△BOC中,BC=![]() ,
,
∴菱形ABCD的周长=4×4![]() =16
=16![]() ;
;
(2)①当点Q在CD边上时,
设PQ交BD于M,则PM=QM,
∵AB∥CD,
∴![]() =1,
=1,
∴BP=DQ,
根据题意得:AP=t,DQ=2t,则BP=4![]() -t,
-t,
∴4![]() -t=2t,
-t=2t,
解得:t=![]() ;
;
当点Q在CB边上时,不存在;
②当点Q在CD边上时,若∠PAQ=90°,如图2所示:
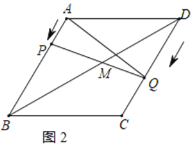
∵AB∥CD,
∴∠AQD=∠PAQ=90°,
∴∠DAQ=30°,
∴DQ=![]() AD=2
AD=2![]() ,
,
即2t=2![]() ,
,
解得:t=![]() ;
;
若∠APQ=90°,如图3所示:

作AN⊥CD于N,则∠PAN=90°,NQ=AP=t,
∴∠DAN=30°,
∴DN=![]() AD=2
AD=2![]() ,
,
∵DQ=DN+NQ,
∴2t=2![]() +t,
+t,
解得:t=2![]() ;
;
当点Q在CB边上时,如图4所示:
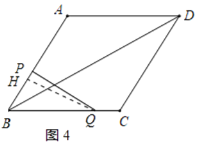
根据题意得:AP=t,BP=4![]() -t,CQ=2t-4
-t,CQ=2t-4![]() ,
,
∴BQ=4![]() -(2t-4
-(2t-4![]() )=8
)=8![]() -2t,
-2t,
∴BP=![]() BQ,
BQ,
作QH⊥BP于H,
∵∠ABC=60°,
∴∠BQH=30°,
∴BH=![]() BQ=4
BQ=4![]() -t,
-t,
∴BP=BH,即H与P重合,
∴∠BPQ=90°,
即∠APQ=90°恒成立.
∴当2![]() ≤t≤4
≤t≤4![]() 时△APQ都为直角三角形.
时△APQ都为直角三角形.
综上可得,当t=![]() 或2
或2![]() ≤t≤4
≤t≤4![]() 时,△APQ恰好为直角三角形.
时,△APQ恰好为直角三角形.


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
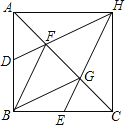
【题目】已知:如图,在△ABC中,AB=BC,∠ABC=90°,点D、E分别是边AB、BC的中点,点F、G是边AC的三等分点,DF、EG的延长线相交于点H,连接HA、HC.
(1)求证:四边形FBGH是菱形;
(2)求证:四边形ABCH是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富同学们的校园生活,某校积极开展了形式多样的社团活动(每人仅限参加一项).小明在八年级随机抽取了2个班级,对这2个班级参加体育类社团活动的人数进行了统计,并绘制了下面的统计图.已知这2个班级共有6%的学生参加“足球”项目,且参加“足球”项目的学生数占参加体育类社团活动学生数的20%.
(1)这2个班参加体育类社团活动人数为 .
(2)请在图中将表示“棒球”项目的图形补充完整;
(2)若该校八年级共有600名学生,请你根据上述信息估计该校八年级共有多少名学生参加“棒球”项目.

查看答案和解析>>
科目:初中数学 来源: 题型:
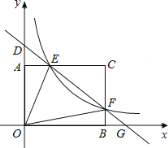
【题目】如图,矩形AOBC的顶点坐标分别为A(0,3),O(0,0),B(4,0),C(4,3),动点F在边BC上(不与B.C重合),过点F的反比例函数y=![]() 的图象与边AC交于点E,直线EF分别与y轴和x轴相交于点D和G.给出下列命题:①若k=4,则△OEF的面积为
的图象与边AC交于点E,直线EF分别与y轴和x轴相交于点D和G.给出下列命题:①若k=4,则△OEF的面积为![]() ;②若k=
;②若k=![]() ,则点C关于直线EF的对称点在x轴上;③满足题设的k的取值范围是0<k≤12;④若DEEG=
,则点C关于直线EF的对称点在x轴上;③满足题设的k的取值范围是0<k≤12;④若DEEG=![]() ,则k=1.其中正确的命题的序号是____________(填序号).
,则k=1.其中正确的命题的序号是____________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
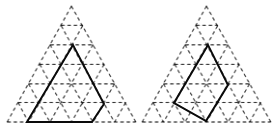
【题目】用水平线和竖起线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数为a,内部的格点个数为b,则S=![]() a+(b-1).
a+(b-1).
对于正三角形网格中的类似问题也有对应结论:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图是该正三角形格点中的两个多边形(设格点多边形的面积为S,该多边形各边上的格点个数为m,内部的格点个数为n):
(1)根据图中提供的信息填表:
m | n-1 | s | |
多边形1 | 11 | ______ | 15 |
多边形2 | 8 | 1 | ______ |
… | … | … | … |
(2)则S与m、m-1之间的关系为______(用含m、n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象与正比例函数
的图象与正比例函数![]() 图象交于点
图象交于点![]() ,且点
,且点![]() 的横坐标为2.
的横坐标为2.
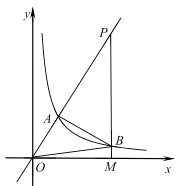
(1)求反比例函数的表达式;
(2)若射线![]() 上有一点
上有一点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 与
与![]() 轴垂直,垂足为
轴垂直,垂足为![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() ,连接
,连接![]() ,
,![]() ,请求出
,请求出![]() 的面积.
的面积.
(3)定义:横纵坐标均为整数的点称为“整点”.在(2)的条件下,请探究边![]() ,
,![]() 与反比例函数图象围成的区域内(不包括边界)“整点”的个数.
与反比例函数图象围成的区域内(不包括边界)“整点”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解学生平均每天“诵读经典”的时间,在全校范围内随机抽查了部分学生进行调查统计,并将调查统计的结果分为四类,每天诵读时间t≤20分钟的学生记为A类,20分钟<t≤40分钟的学生记为B类,40分钟<t≤60分钟的学生记为C类,t>60分钟的学生记为D类.将收集的数据绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:

(1)这次共抽查了 名学生进行调查统计,m= ,n= ;
(2)请补全上面的条形图;
(3)如果该校共有1600名学生,请你估计该校C类学生约有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com