
【题目】用水平线和竖起线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数为a,内部的格点个数为b,则S=![]() a+(b-1).
a+(b-1).
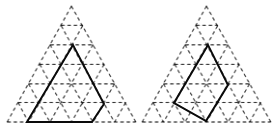
对于正三角形网格中的类似问题也有对应结论:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图是该正三角形格点中的两个多边形(设格点多边形的面积为S,该多边形各边上的格点个数为m,内部的格点个数为n):
(1)根据图中提供的信息填表:
m | n-1 | s | |
多边形1 | 11 | ______ | 15 |
多边形2 | 8 | 1 | ______ |
… | … | … | … |
(2)则S与m、m-1之间的关系为______(用含m、n的代数式表示).
科目:初中数学 来源: 题型:
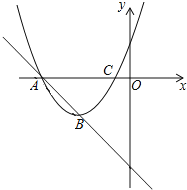
【题目】如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于A、B两个不同的点,其中点A在x轴上.
(1)n=3m-9(用含m的代数式表示);
(2)若点B为该抛物线的顶点,求m、n的值;
(3)①设m=-2,当-3≤x≤0时,求二次函数y=x2+mx+n的最小值;
②若-3≤x≤0时,二次函数y=x2+mx+n的最小值为-4,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
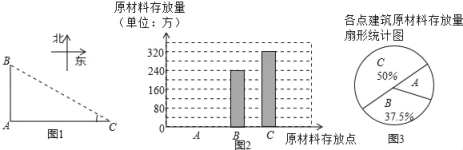
【题目】重庆八中将于2017年整体搬迁至渝北空港新城,新校园工程建设正在如火如荼的进行.经工程部管理人员同意,四位同学前往工地进行社会实践活动.如图,A、B、C是三个建筑原材料存放点,点B、C分别位于点A的正北和正东方向,AC=400米.四人分别测得∠C的度数如表:
甲 | 乙 | 丙 | 丁 | |
∠C(单位:度) | 34 | 36 | 38 | 40 |
他们又调查了各点的建筑材料存放量,并绘制了下列尚不完整的统计如图、如图:
(1)求表中∠C度数的平均数![]() ;
;
(2)求A处的建筑原材料存放量,并将如图补充完整;
(3)用(1)中的![]() 作为∠C的度数,要将A处的全部建筑原材料沿道路AB运到B处,已知运1方建筑原材料每米的费用为0.1元,求运完全部建筑原材料所需的费用.(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
作为∠C的度数,要将A处的全部建筑原材料沿道路AB运到B处,已知运1方建筑原材料每米的费用为0.1元,求运完全部建筑原材料所需的费用.(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
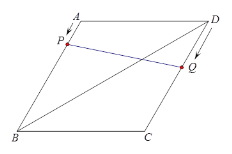
【题目】如图,在菱形ABCD中,已知∠BAD=120°,对角线BD长为12.
(1)求菱形ABCD的周长;
(2)动点P从点A出发,沿A→B的方向,以每秒1个单位的速度向点B运动;在点P出发的同时,动点Q从点D出发,沿D→C→B的方向,以每秒2个单位的速度向点B运动.设运动时间为t(s).
①当PQ恰好被BD平分时,试求t的值;
②连接AQ,试求:在整个运动过程中,当t取怎样的值时,△APQ恰好是一个直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
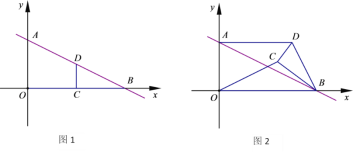
【题目】如图,在平面直角坐标系中,直线l:![]() 与x轴.y轴交于B,A两点,点D,C分别为线段AB,OB的中点,连结CD,如图,将△DCB绕点B按顺时针方向旋转角
与x轴.y轴交于B,A两点,点D,C分别为线段AB,OB的中点,连结CD,如图,将△DCB绕点B按顺时针方向旋转角![]() ,如图.
,如图.
(1)连结OC,AD,求证![]() ∽
∽![]() ;
;
(2)当0°<![]() <180°时,若△DCB旋转至A,C,D三点共线时,求线段OD的长;
<180°时,若△DCB旋转至A,C,D三点共线时,求线段OD的长;
(3)试探索:180°<![]() <360°时,是否还有可能存在A,C,D三点共线的情况,若存在,求出此直线的表达式;若不存在,请说明理由.
<360°时,是否还有可能存在A,C,D三点共线的情况,若存在,求出此直线的表达式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某度假村拥有客房40间,该度假村在经营中发现每间客房日租金x(元)与每日租出的客房数(y)有如下关系:
x | 200 | 220 | 260 | 280 |
y | 40 | 35 | 25 | 20 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每日租出的客房数y(间)与每间客房的日租金x(元)之间的关系式.
(2)已知租出的每间客房每日需要清洁费80元,未租出的每间客房每日需要清洁费40元.含x(x≥200)的代数式填表:
租出的客房数 | ______ | 未租出的客房数 | ______ |
租出的每间客房的日收益 | ______ | 所有未租出的客房每日的清洁费 | ______ |
(3)若你是该度假村的老板,你会将每间客房的日租金定为多少元,才能使度假村获得最大日收益?最大日收益是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
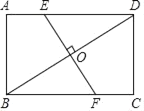
【题目】如图,在矩形ABCD中,AB=3cm,AD=4cm,EF经过对角线BD的中点O,分别交AD,BC于点E,F.
(1)求证:△BOF≌△DOE;
(2)当EF⊥BD时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
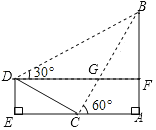
【题目】如图,小明想测量斜坡![]() 旁一棵垂直于地面
旁一棵垂直于地面![]() 的树
的树![]() 的高度,他们先在点
的高度,他们先在点![]() 处测得树顶
处测得树顶![]() 的仰角为
的仰角为![]() ,然后在坡顶
,然后在坡顶![]() 测得树顶
测得树顶![]() 的仰角为
的仰角为![]() ,已知斜坡
,已知斜坡![]() 的长度为
的长度为![]() ,斜坡顶点
,斜坡顶点![]() 到地面的垂直高度
到地面的垂直高度![]() ,则树
,则树![]() 的高度是( )
的高度是( )![]()
A. 20![]() B. 30
B. 30![]() C. 30D. 40
C. 30D. 40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数
,1)在反比例函数![]() 的图象上.
的图象上.

(1)求反比例函数![]() 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP=![]() S△AOB,求点P的坐标;
S△AOB,求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com