
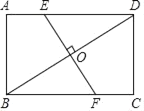
【题目】如图,在矩形ABCD中,AB=3cm,AD=4cm,EF经过对角线BD的中点O,分别交AD,BC于点E,F.
(1)求证:△BOF≌△DOE;
(2)当EF⊥BD时,求AE的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据已知条件易证∠BFO=∠DEO,∠FBO=∠EDO,OB=OD,再利用AAS证明△BOF≌△DOE即可;(2)连接BE,设AE=xcm,由EB=ED=AD﹣AE=(4﹣x)cm,在Rt△ABE中,根据AB2+AE=BE2,构建方程即可解决问题.
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BFO=∠DEO,∠FBO=∠EDO,
又∵O是BD中点,
∴OB=OD,
∴△BOF≌△DOE(ASA).
(2)连接BE.
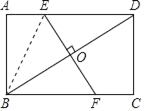
∵EF⊥BD,O为BD中点,
∴EB=ED,
设AE=xcm,由EB=ED=AD﹣AE=(4﹣x)cm,
在Rt△ABE中,AB=3cm,
根据勾股定理得:AB2+AE=BE2,即9+x2=(4﹣x)2,
解得:x=![]() ,
,
∴AE的长是 ![]() cm.
cm.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】为丰富同学们的校园生活,某校积极开展了形式多样的社团活动(每人仅限参加一项).小明在八年级随机抽取了2个班级,对这2个班级参加体育类社团活动的人数进行了统计,并绘制了下面的统计图.已知这2个班级共有6%的学生参加“足球”项目,且参加“足球”项目的学生数占参加体育类社团活动学生数的20%.
(1)这2个班参加体育类社团活动人数为 .
(2)请在图中将表示“棒球”项目的图形补充完整;
(2)若该校八年级共有600名学生,请你根据上述信息估计该校八年级共有多少名学生参加“棒球”项目.

查看答案和解析>>
科目:初中数学 来源: 题型:
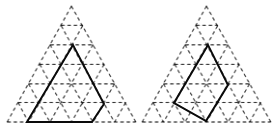
【题目】用水平线和竖起线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数为a,内部的格点个数为b,则S=![]() a+(b-1).
a+(b-1).
对于正三角形网格中的类似问题也有对应结论:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图是该正三角形格点中的两个多边形(设格点多边形的面积为S,该多边形各边上的格点个数为m,内部的格点个数为n):
(1)根据图中提供的信息填表:
m | n-1 | s | |
多边形1 | 11 | ______ | 15 |
多边形2 | 8 | 1 | ______ |
… | … | … | … |
(2)则S与m、m-1之间的关系为______(用含m、n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系中有两点A(0,1),B(![]() ,0),动点P在线段AB上运动,过点P作y轴的垂线,垂足为点M,作x轴的垂线,垂足为点N,连接MN,则线段MN的最小值为( )
,0),动点P在线段AB上运动,过点P作y轴的垂线,垂足为点M,作x轴的垂线,垂足为点N,连接MN,则线段MN的最小值为( )
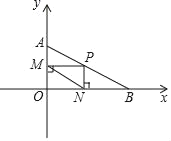
A. 1B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象与正比例函数
的图象与正比例函数![]() 图象交于点
图象交于点![]() ,且点
,且点![]() 的横坐标为2.
的横坐标为2.
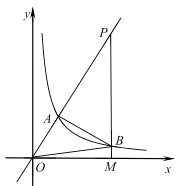
(1)求反比例函数的表达式;
(2)若射线![]() 上有一点
上有一点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 与
与![]() 轴垂直,垂足为
轴垂直,垂足为![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() ,连接
,连接![]() ,
,![]() ,请求出
,请求出![]() 的面积.
的面积.
(3)定义:横纵坐标均为整数的点称为“整点”.在(2)的条件下,请探究边![]() ,
,![]() 与反比例函数图象围成的区域内(不包括边界)“整点”的个数.
与反比例函数图象围成的区域内(不包括边界)“整点”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三一班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲队 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙队 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是_________分,乙队成绩的众数是_________分;
(2)已知甲队成绩的方差是1.4分2,则成绩较为整齐的是_________队;
(3)测试结果中,乙队获满分的四名同学相当优秀,他们是三名男生、一名女生,现准备从这四名同学中随机抽取两人参加学校组织的经典诵读比赛,用树状图或列表法求恰好抽中一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
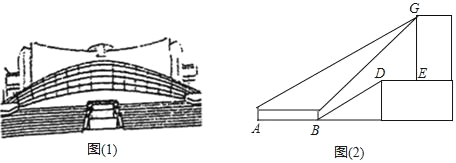
【题目】如图(1)是重庆中国三峡博物馆,又名重庆博物馆,中央地方共建国家级博物馆图(2)是侧面示意图.某校数学兴趣小组的同学要测量三峡博物馆的高GE.如(2),小杰身高为1.6米,小杰在A处测得博物馆楼顶G点的仰角为27°,前进12米到达B处测得博物馆楼顶G点的仰角为39°,斜坡BD的坡i=1:2.4,BD长度是13米,GE⊥DE,A、B、D、E、G在同一平面内,则博物馆高度GE约为_____米.(结果精确到1米,参考数据tan27°≈0.50,tan39°≈0.80)
查看答案和解析>>
科目:初中数学 来源: 题型:
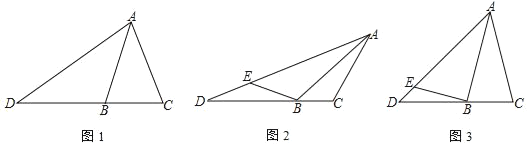
【题目】在△ABC中,D是CB延长线上一点,∠BAD=∠BAC.
(1)如图,求证:![]() ;
;
(2)如图,在AD上有一点E,∠EBA=∠ACB=120°.若AC=2BC=2,求DE的长;
(3)如图,若AB=AC=2BC=4,BE⊥AB交AD于点E,直接写出△BDE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com