
����Ŀ��Ϊ�ḻͬѧ�ǵ�У���ijУ������չ����ʽ���������Ż��ÿ�˽��μ�һ���С���ڰ��꼶�����ȡ��2���༶������2���༶�μ����������Ż������������ͳ�ƣ��������������ͳ��ͼ����֪��2���༶����6%��ѧ���μ�����������Ŀ���Ҳμ�����������Ŀ��ѧ����ռ�μ����������Żѧ������20%��
��1����2����μ����������Ż����Ϊ ��
��2������ͼ�н���ʾ����������Ŀ��ͼ�β���������
��2������У���꼶����600��ѧ�����������������Ϣ���Ƹ�У���꼶���ж�����ѧ���μ�����������Ŀ��

���𰸡���1��30����2������Ϊ4�� ��3��24���ˣ���
��������
��1�����ݲμ�����������Ŀ��ѧ����ռ�μ����������Żѧ������20%�����ɵõ�2����μ����������Ż������
��2�����ݱ�ʾ����������Ŀ�����������ɽ���ʾ����������Ŀ��ͼ�β���������
��3�����ݲμ�����������Ŀ��������ռ�İٷֱȣ����ɹ��Ƹ�У���꼶���ж�����ѧ���μ�����������Ŀ��
�⣺��1��2����μ����������Ż����Ϊ6��20%=30���ˣ���
�ʴ�Ϊ��30��
��2����ʾ����������Ŀ������Ϊ��30-10-10-6=4���ˣ���
��ͼ��ʾ��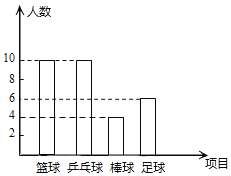
��3��600��![]() =24���ˣ���
=24���ˣ���
�𣺸�У���꼶����24��ѧ���μ�����������Ŀ��


 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ĸ���ȫ��ͬ��С���Ϸֱ�д��1��2��3��4�ĸ����֣�Ȼ��װ��һ�������Ŀڴ��ڽ��ȣ��ӿڴ���ȡ��һ����������ֺ���Ϊ��M�ĺ�����x���Żش��н��ȣ�Ȼ���ٴӴ���ȡ��һ����������ֺ���Ϊ��M��������y�����M��x��y������ֱ��y����x+5�ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ӽ�������ʻ���ҵأ�һ���쳵ͬʱ���ҵس���������ʻ���أ�����֮��ľ���y��ǧ�ף�����ʻʱ��x��Сʱ���Ķ�Ӧ��ϵ��ͼ��ʾ������������ȷ���ǣ� ��
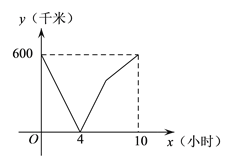
A. �����������1200ǧ��
B. �쳵���ٶ���80ǧ���MСʱ
C. �������ٶ���60ǧ���MСʱ
D. �쳵�����ʱ�����������ҵ�100ǧ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
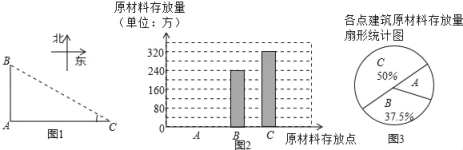
����Ŀ��������н���2017�������Ǩ���山�ո��³ǣ���У���̽������������ݱ�Ľ��У������̲�������Աͬ�⣬��λͬѧǰ�����ؽ������ʵ�������ͼ��A��B��C����������ԭ���ϴ�ŵ㣬��B��C�ֱ�λ�ڵ�A����������������AC��400�ף����˷ֱ��á�C�Ķ��������
�� | �� | �� | �� | |
��C����λ���ȣ� | 34 | 36 | 38 | 40 |
�����ֵ����˸���Ľ������ϴ�������������������в�������ͳ����ͼ����ͼ��
��1������С�C������ƽ����![]() ��
��
��2����A���Ľ���ԭ���ϴ������������ͼ����������
��3���ã�1���е�![]() ��Ϊ��C�Ķ�����Ҫ��A����ȫ������ԭ�����ص�·AB�˵�B������֪��1������ԭ����ÿ�ķ���Ϊ0.1Ԫ��������ȫ������ԭ��������ķ��ã���ע��sin37����0.6��cos37����0.8��tan37����0.75��
��Ϊ��C�Ķ�����Ҫ��A����ȫ������ԭ�����ص�·AB�˵�B������֪��1������ԭ����ÿ�ķ���Ϊ0.1Ԫ��������ȫ������ԭ��������ķ��ã���ע��sin37����0.6��cos37����0.8��tan37����0.75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
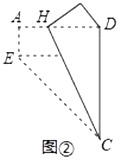
����Ŀ����1�����������֣�����ͼһ���ھ���ABCD�У�E��BC���е㣬����ABE��AE�۵���õ���AFE����F�ھ���ABCD�ڲ����ӳ�AF��CD�ڵ�G�������߶�GF��GC��������ϵ���� ����
��2�������̽��������ͼ��������1���еľ���ABCD��Ϊƽ���ı��Σ������������䣬��1���еĽ����Ƿ���Ȼ��������˵�����ɣ�
��3����Ӧ�ã�����ͼ��������1���еľ���ABCD��Ϊ�����Σ��߳�AB��4�������������䣬���߶�GC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
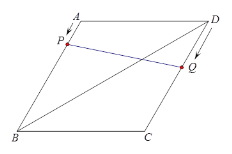
����Ŀ����ͼ��������ABCD�У���֪��BAD��120�����Խ���BD��Ϊ12��
��1��������ABCD���ܳ���
��2������P�ӵ�A��������A��B�ķ�����ÿ��1����λ���ٶ����B�˶����ڵ�P������ͬʱ������Q�ӵ�D��������D��C��B�ķ�����ÿ��2����λ���ٶ����B�˶������˶�ʱ��Ϊt��s����
�ٵ�PQǡ�ñ�BDƽ��ʱ������t��ֵ��
������AQ�������������˶������У���tȡ������ֵʱ����APQǡ����һ��ֱ�������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
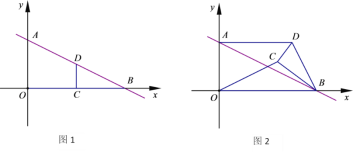
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l��![]() ��x��.y�ύ��B��A���㣬��D��C�ֱ�Ϊ�߶�AB��OB���е㣬����CD����ͼ������DCB�Ƶ�B��˳ʱ�뷽����ת��
��x��.y�ύ��B��A���㣬��D��C�ֱ�Ϊ�߶�AB��OB���е㣬����CD����ͼ������DCB�Ƶ�B��˳ʱ�뷽����ת��![]() ����ͼ��
����ͼ��
(1)����OC��AD����֤![]() ��
��![]() ��
��
(2)��0��<![]() <180��ʱ������DCB��ת��A��C��D���㹲��ʱ�����߶�OD�ij���
<180��ʱ������DCB��ת��A��C��D���㹲��ʱ�����߶�OD�ij���
(3)��̽����180��<![]() <360��ʱ���Ƿ��п��ܴ���A��C��D���㹲�ߵ�����������ڣ������ֱ�ߵı���ʽ���������ڣ���˵�����ɣ�
<360��ʱ���Ƿ��п��ܴ���A��C��D���㹲�ߵ�����������ڣ������ֱ�ߵı���ʽ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
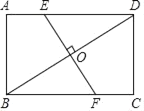
����Ŀ����ͼ���ھ���ABCD�У�AB��3cm��AD��4cm��EF�����Խ���BD���е�O���ֱ�AD��BC�ڵ�E��F��
��1����֤����BOF�ա�DOE��
��2����EF��BDʱ����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
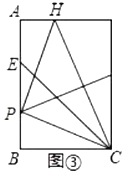
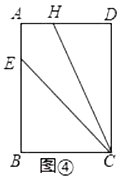
����Ŀ���Ը�����һ�ž���ֽƬ![]() �������²���������
�������²���������![]() �۵���ʹ��
�۵���ʹ��![]() ����
����![]() ����(��ͼ��)������
����(��ͼ��)������![]() �۵�����ʱ���ֵ�
�۵�����ʱ���ֵ�![]() ǡ�����
ǡ�����![]() �غ�(��ͼ��)
�غ�(��ͼ��)
(1)�������ϲ����ͷ��֣���![]() ____��
____��
(2)���þ���ֽƬչ������ͼ�ۣ��۵��þ���ֽƬ��ʹ��![]() ���
���![]() �غϣ��ۺ���
�غϣ��ۺ���![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ���ٽ��þ���ֽƬչ����
���ٽ��þ���ֽƬչ����
��֤��![]() ��
��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com