
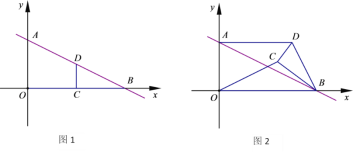
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l��![]() ��x��.y�ύ��B��A���㣬��D��C�ֱ�Ϊ�߶�AB��OB���е㣬����CD����ͼ������DCB�Ƶ�B��˳ʱ�뷽����ת��
��x��.y�ύ��B��A���㣬��D��C�ֱ�Ϊ�߶�AB��OB���е㣬����CD����ͼ������DCB�Ƶ�B��˳ʱ�뷽����ת��![]() ����ͼ��
����ͼ��
(1)����OC��AD����֤![]() ��
��![]() ��
��
(2)��0��<![]() <180��ʱ������DCB��ת��A��C��D���㹲��ʱ�����߶�OD�ij���
<180��ʱ������DCB��ת��A��C��D���㹲��ʱ�����߶�OD�ij���
(3)��̽����180��<![]() <360��ʱ���Ƿ��п��ܴ���A��C��D���㹲�ߵ�����������ڣ������ֱ�ߵı���ʽ���������ڣ���˵�����ɣ�
<360��ʱ���Ƿ��п��ܴ���A��C��D���㹲�ߵ�����������ڣ������ֱ�ߵı���ʽ���������ڣ���˵�����ɣ�
���𰸡���1�������������2��![]() ��3�����ڣ�
��3�����ڣ�![]()
��������
��1����ȷ������A��B���꣬�������BC��CD�������жϳ���OBC�ס�ABD��
��2����ȷ������ACB�ա�BOA�������жϳ�ƽ���ı���AOBC�Ǿ��Σ����ù��ɶ������ɵó����ۣ�
��3�������![]() ���������ù��ɶ��������C�����꣨
���������ù��ɶ��������C�����꣨![]() ��
��![]() ��������ô���ϵ�������ɵó����ۣ�
��������ô���ϵ�������ɵó����ۣ�
�⣺(1)��![]() ��A(0��4),B(8��0)��
��A(0��4),B(8��0)��
��OA=4��OB=8��
��AD=BD,OC=BC
��![]() BC=4��
BC=4��![]()
�ߡ�ABO=��DBC,
���ABO+��ABC=��DBC+��ABC.
���OBC=��ABD��
��.��![]()
���OBC�ס�ABD.
(2)��0��<![]() <180������A,C,D���㹲��ʱ����ͼ��
<180������A,C,D���㹲��ʱ����ͼ��
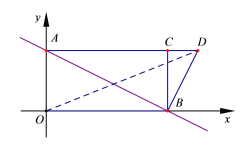
�ߡ�BCD=90��,
���ACB=90��.
���ACB=��BOA=90��.
�֡�OA=BC=4��AB=BA,
���ACB�ա�BOA.
��AC=BO.
���ı���AOBC��ƽ���ı��� �֡ߡ�AOB=90��.
��ƽ���ı���AOBC�Ǿ���.
���AOC=90����AC=OB=8.
��AD=AC+CD=8+2=10.
��![]()
(3)����.
��180��<![]() <360����A,C,D���㹲��ʱ����ͼ��
<360����A,C,D���㹲��ʱ����ͼ��
����OC,ͬ��1���ɵã���ABD�ס�BOC.
��![]()
ͬ��2���ɵã���ACB�ա�BOA.
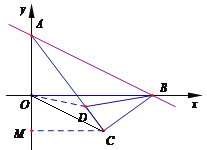
��AC=BO=8.
��CD=2����AD=6.
��![]()
��![]()
��![]()
����C��CM��y����M����OM=y��MC=x.
��Rt��OMC��Rt��AMC����
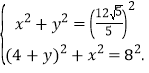 ��ã�
��ã�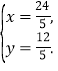
���C�����꣨![]() ��
��![]() ����
����
��ֱ��AC�ı���ʽΪ![]()
��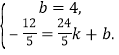 ��ã�
��ã�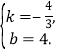
��������ֱ��AC�ı���ʽΪ![]()


 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽���������ѧ�������Ķ����������С���������ѧ�ڳ���ѧ���Ķ������鼮�IJ��������˳������飬�����ݵ��������Ƴ�����ͳ��ͼ��
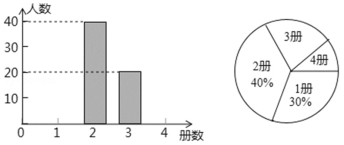
����ͳ��ͼ�ṩ����Ϣ������������⣺
��1������������������������ ����
��2����ȫ����ͳ��ͼ��
��3����������18000����������������������ѧ����ѧ�ڿ����Ķ�����2���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
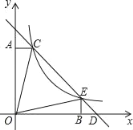
����Ŀ����ͼ��ֱ��y����x+b�뷴��������y��![]() ��k��0����ͼ���һ֧����C��1��4����E���㣬CA��y���ڵ�A��EB��x���ڵ�B�������½��ۣ���k��ֵΪ4������BED�ǵ���ֱ�������Σ���S��ACO��S��BEO����S��CEO��15���ݵ�D������Ϊ��5��0����������ȷ���ǣ�������
��k��0����ͼ���һ֧����C��1��4����E���㣬CA��y���ڵ�A��EB��x���ڵ�B�������½��ۣ���k��ֵΪ4������BED�ǵ���ֱ�������Σ���S��ACO��S��BEO����S��CEO��15���ݵ�D������Ϊ��5��0����������ȷ���ǣ�������
A. �٢ڢ�B. �٢ڢۢ�C. �ڢۢܢ�D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ḻͬѧ�ǵ�У���ijУ������չ����ʽ���������Ż��ÿ�˽��μ�һ���С���ڰ��꼶�����ȡ��2���༶������2���༶�μ����������Ż������������ͳ�ƣ��������������ͳ��ͼ����֪��2���༶����6%��ѧ���μ�����������Ŀ���Ҳμ�����������Ŀ��ѧ����ռ�μ����������Żѧ������20%��
��1����2����μ����������Ż����Ϊ ��
��2������ͼ�н���ʾ����������Ŀ��ͼ�β���������
��2������У���꼶����600��ѧ�����������������Ϣ���Ƹ�У���꼶���ж�����ѧ���μ�����������Ŀ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
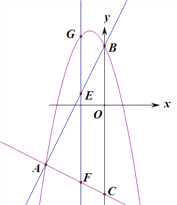
����Ŀ����ͼ��������y=-x2+bx+c��ֱ��AB����A(-4��-4)��B(0��4)���㣬ֱ��AC��y=-![]() x-6��y�����C.��E��ֱ��AB�ϵĶ��㣬����E��EF��x�ύAC�ڵ�F�����������ڵ�G.
x-6��y�����C.��E��ֱ��AB�ϵĶ��㣬����E��EF��x�ύAC�ڵ�F�����������ڵ�G.
��1����������y=-x2+bx+c�ı���ʽ��
��2������GB��EO�����ı���GEOB��ƽ���ı���ʱ�����G�����ꣻ
��3������y���ϴ���һ��H������EH��HF������E�˶���ʲôλ��ʱ����A��E��F��HΪ������ı����Ǿ��Σ������ʱ��E��H�����ꣻ
���ڢٵ�ǰ���£��Ե�EΪԲ�ģ�EH��Ϊ�뾶��Բ����MΪ��E��һ���㣬��![]() AM+CM����Сֵ.
AM+CM����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ˮƽ�ߺ������߽�ƽ��ֳ����ɸ��߳�Ϊ1��С�����θ��ӣ�С�����εĶ����Ϊ��㣬�Ը��Ϊ����Ķ���γ�Ϊ������Σ��������ε����ΪS���ö���θ����ϵĸ�����Ϊa���ڲ��ĸ�����Ϊb����S=![]() a+(b-1)��
a+(b-1)��
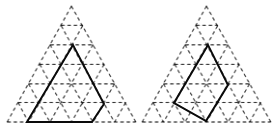
�����������������е���������Ҳ�ж�Ӧ���ۣ���������������ÿ��С�����������Ϊ1��С�������εĶ���Ϊ��㣬�Ը��Ϊ����Ķ���γ�Ϊ������Σ���ͼ�Ǹ��������θ���е����������(�������ε����ΪS���ö���θ����ϵĸ�����Ϊm���ڲ��ĸ�����Ϊn)��
(1)����ͼ���ṩ����Ϣ�����
m | n-1 | s | |
�����1 | 11 | ______ | 15 |
�����2 | 8 | 1 | ______ |
�� | �� | �� | �� |
(2)��S��m��m-1֮��Ĺ�ϵΪ______(�ú�m��n�Ĵ���ʽ��ʾ)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
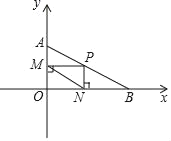
����Ŀ����ͼ����֪��ƽ��ֱ������ϵ��������A��0��1����B��![]() ��0��������P���߶�AB���˶�������P��y��Ĵ��ߣ�����Ϊ��M����x��Ĵ��ߣ�����Ϊ��N������MN�����߶�MN����СֵΪ��������
��0��������P���߶�AB���˶�������P��y��Ĵ��ߣ�����Ϊ��M����x��Ĵ��ߣ�����Ϊ��N������MN�����߶�MN����СֵΪ��������
A. 1B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ����һ����֯��һ�ξ����ж��������ס������Ӹ�10�˵ı����ɼ����±���10���ƣ���
�� | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
�Ҷ� | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
��1���ӳɼ�����λ����_________�֣��Ҷӳɼ���������_________�֣�
��2����֪�ӳɼ��ķ�����1.4��2����ɼ���Ϊ�������_________�ӣ�
��3�����Խ���У��Ҷӻ����ֵ�����ͬѧ�൱���㣬����������������һ��Ů����������������ͬѧ�������ȡ���˲μ�ѧУ��֯�ľ����ж�����������״ͼ���б�����ǡ�ó���һ����һŮ���ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
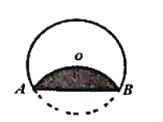
����Ŀ����ͼ���Ѱ뾶Ϊ![]() ��
��![]() ����
����![]() �۵���
�۵���![]() ����Բ��
����Բ��![]() ������Ӱ���ֵ����Ϊ__________�����������
������Ӱ���ֵ����Ϊ__________�����������![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com