
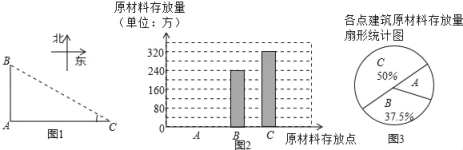
����Ŀ��������н���2017�������Ǩ���山�ո��³ǣ���У���̽������������ݱ�Ľ��У������̲�������Աͬ�⣬��λͬѧǰ�����ؽ������ʵ�������ͼ��A��B��C����������ԭ���ϴ�ŵ㣬��B��C�ֱ�λ�ڵ�A����������������AC��400�ף����˷ֱ��á�C�Ķ��������
�� | �� | �� | �� | |
��C����λ���ȣ� | 34 | 36 | 38 | 40 |
�����ֵ����˸���Ľ������ϴ�������������������в�������ͳ����ͼ����ͼ��
��1������С�C������ƽ����![]() ��
��
��2����A���Ľ���ԭ���ϴ������������ͼ����������
��3���ã�1���е�![]() ��Ϊ��C�Ķ�����Ҫ��A����ȫ������ԭ�����ص�·AB�˵�B������֪��1������ԭ����ÿ�ķ���Ϊ0.1Ԫ��������ȫ������ԭ��������ķ��ã���ע��sin37����0.6��cos37����0.8��tan37����0.75��
��Ϊ��C�Ķ�����Ҫ��A����ȫ������ԭ�����ص�·AB�˵�B������֪��1������ԭ����ÿ�ķ���Ϊ0.1Ԫ��������ȫ������ԭ��������ķ��ã���ע��sin37����0.6��cos37����0.8��tan37����0.75��
���𰸡���1��![]() ��37���ȣ�����2��ԭ���ϵ��ܴ������640������A���Ĵ������80������3������ȫ������ԭ��������ķ�����2400Ԫ��
��37���ȣ�����2��ԭ���ϵ��ܴ������640������A���Ĵ������80������3������ȫ������ԭ��������ķ�����2400Ԫ��
��������
��1������ƽ������ʽ������⣻
��2������C�ֲ�����320����ռ50%����������ܷ����������ܷ������Զ�Ӧ�İٷֱȼ������A���Ĵ������
��3������A���Ĵ��������AB�ij��ٳ���0.1���ɣ�
��1��![]() ��
��![]() ��34+36+38+40����37���ȣ���
��34+36+38+40����37���ȣ���
��2��ԭ���ϵ��ܴ�����ǣ�320��50%��640��������
����A���Ĵ�����ǣ�640��1��50%��37.5%����80��������
 ��
��
��3������ֱ����ABC�У�tanC��![]() ��
��
��AB��ACtan37����400��0.75��300���ף���
������ȫ������ԭ��������ķ����ǣ�80��300��0.1��2400��Ԫ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������ABCD����EAF��45����
��1����ͼ������E��F�ֱ��ڱ�BC��CD�ϣ�����EF����֤��EF��BE+DF��
ͯ��ͬѧ������˼���ģ��������һ��������½��֤��������ADF�Ƶ�A˳ʱ����ת90��������ABG��������ADF�ա�ABG��
��2����ͼ����M��N�ֱ��ڱ�AB��CD�ϣ���BN��DM������E��F�ֱ���BM��DN�ϣ�����EF��̽�������߶�EF��BE��DF֮�������������ϵ����֤�����Ľ��ۣ�
��3����ͼ������E��F�ֱ��ڶԽ���BD����CD�ϣ���FC��2����BE�ij�Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���߳�Ϊ������ֱ�������Σ�������ֱ�DZ߱߳��Ƿ���x2-(k+2)x+4k=0����������k��ֵ����ȷ��ֱ������������֮����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
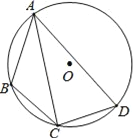
����Ŀ����ͼ���ڡ�O���ڽ��ı���ABCD�У�AB=3��AD=5����BAD=60������CΪ��BD���е㣬��AC�ij���__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y����x+b�뷴��������y��![]() ��k��0����ͼ���һ֧����C��1��4����E���㣬CA��y���ڵ�A��EB��x���ڵ�B�������½��ۣ���k��ֵΪ4������BED�ǵ���ֱ�������Σ���S��ACO��S��BEO����S��CEO��15���ݵ�D������Ϊ��5��0����������ȷ���ǣ�������
��k��0����ͼ���һ֧����C��1��4����E���㣬CA��y���ڵ�A��EB��x���ڵ�B�������½��ۣ���k��ֵΪ4������BED�ǵ���ֱ�������Σ���S��ACO��S��BEO����S��CEO��15���ݵ�D������Ϊ��5��0����������ȷ���ǣ�������
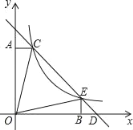
A. �٢ڢ�B. �٢ڢۢ�C. �ڢۢܢ�D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�MΪBC��һ�㣬F��AM���е㣬EF��AM������ΪF����AD���ӳ����ڵ�E����DC�ڵ�N��

��1����֤����ABM�ס�EFA��
��2����AB=12��BM=5����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ḻͬѧ�ǵ�У���ijУ������չ����ʽ���������Ż��ÿ�˽��μ�һ���С���ڰ��꼶�����ȡ��2���༶������2���༶�μ����������Ż������������ͳ�ƣ��������������ͳ��ͼ����֪��2���༶����6%��ѧ���μ�����������Ŀ���Ҳμ�����������Ŀ��ѧ����ռ�μ����������Żѧ������20%��
��1����2����μ����������Ż����Ϊ ��
��2������ͼ�н���ʾ����������Ŀ��ͼ�β���������
��2������У���꼶����600��ѧ�����������������Ϣ���Ƹ�У���꼶���ж�����ѧ���μ�����������Ŀ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
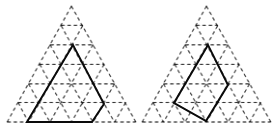
����Ŀ����ˮƽ�ߺ������߽�ƽ��ֳ����ɸ��߳�Ϊ1��С�����θ��ӣ�С�����εĶ����Ϊ��㣬�Ը��Ϊ����Ķ���γ�Ϊ������Σ��������ε����ΪS���ö���θ����ϵĸ�����Ϊa���ڲ��ĸ�����Ϊb����S=![]() a+(b-1)��
a+(b-1)��
�����������������е���������Ҳ�ж�Ӧ���ۣ���������������ÿ��С�����������Ϊ1��С�������εĶ���Ϊ��㣬�Ը��Ϊ����Ķ���γ�Ϊ������Σ���ͼ�Ǹ��������θ���е����������(�������ε����ΪS���ö���θ����ϵĸ�����Ϊm���ڲ��ĸ�����Ϊn)��
(1)����ͼ���ṩ����Ϣ�����
m | n-1 | s | |
�����1 | 11 | ______ | 15 |
�����2 | 8 | 1 | ______ |
�� | �� | �� | �� |
(2)��S��m��m-1֮��Ĺ�ϵΪ______(�ú�m��n�Ĵ���ʽ��ʾ)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1���������й���Ͽ����ݣ��������첩��ݣ�����ط��������Ҽ������ͼ��2���Dz���ʾ��ͼ��ijУ��ѧ��ȤС���ͬѧҪ������Ͽ����ݵĸ�GE���磨2����С������Ϊ1.6�ף�С����A����ò����¥��G�������Ϊ27����ǰ��12����B����ò����¥��G�������Ϊ39����б��BD����i��1��2.4��BD������13�ף�GE��DE��A��B��D��E��G��ͬһƽ���ڣ�����ݸ߶�GEԼΪ_____�ף��������ȷ��1�ף��ο�����tan27���0.50��tan39���0.80��
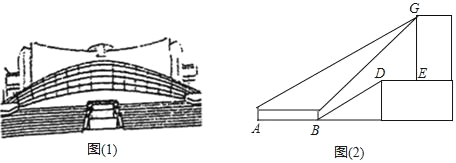
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com