
【题目】已知多项式2ax4+5ax3-13x2-x4+2021+2x+bx3-bx4-13x3是二次多项式,则a2+b2=。
【答案】13
【解析】解:∵2ax4+5ax3-13x2-x4+2021+2x+bx3-bx4-13x3=(2a-b-1)x ![]() +(5a-13+b)x
+(5a-13+b)x ![]() -13x
-13x ![]() +2x+2021,
+2x+2021,
又∵此多项式为二次多项式,
∴ ![]() ,
,
解得 ![]() .
.
所以a ![]() +b
+b ![]() =2
=2 ![]() +3
+3 ![]() =13.
=13.
故答案为13.
将多项式2ax4+5ax3-13x2-x4+2021+2x+bx3-bx4-13x3进行合并得出(2a-b-1)x 4 +(5a-13+b)x 3 -13x 2 +2x+2021,又根据此多项式是二次多项式,从而得出关于a,b的方程,2a-b-1=0,5a-13+b=0;解它们组成的方程组,即可得出a,b的值,再代入代数式计算出结果即可。


科目:初中数学 来源: 题型:
【题目】某玩具专柜要经营一种新上市的儿童玩具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)写出专柜销售这种玩具,每天所得的销售利润W(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该玩具每天的销售利润最大;
(3)专柜结合上述情况,设计了A、B两种营销方案:
方案A:该玩具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件玩具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AB∥DE,AF∥DC,E、F两点在边BC上,且四边形AEFD是平行四边形. 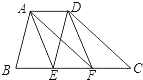
(1)AD与BC有何等量关系,请说明理由;
(2)当AB=DC时,求证:平行四边形AEFD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一箱苹果分给若干个小朋友,若每位小朋友分5个苹果,则还剩12个苹果;若每位小朋友分8个苹果,则有一个小朋友能分到不足5个苹果.这一箱苹果的个数是 , 小朋友的人数是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】In right Fig.,if the length of the segment AB is 1,M is the midpoint of the segment AB,and point C divides the segment MB into two parts such that MC:CB=1:2,then the length of AC is 。
(英汉词典:length 长度;segment 线段;midpoint 中点;divides…into 分为,分成)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4). 
①画出△ABC向左平移5个单位长度后得到的△A1B1C1;
②请画出△ABC关于原点对称的△A2B2C2 , 并写出点A2、B2、C2坐标;
③请画出△ABC绕原点O逆时针旋转90°后△A3B3C3 , 并写出点A3、B3、C3坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】满足下列条件的三角形中,不是直角三角形的是( )
A.三内角之比为1:2:3
B.三边长分别为5,12,14
C.三边长之比为3:4:5
D.三边长分别为1, ![]() ,
, ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB,BD于M,N两点.若AM=2,则线段ON的长为( ) 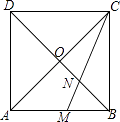
A.![]()
B.![]()
C.1
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com