
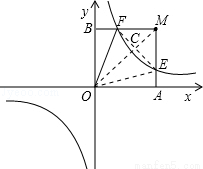
已知双曲线y=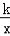 (k>0),过点M(m,m)(m>
(k>0),过点M(m,m)(m> )作MA⊥x轴,MB⊥y轴,垂足分别是A和B,MA、MB分别交双曲线y=
)作MA⊥x轴,MB⊥y轴,垂足分别是A和B,MA、MB分别交双曲线y=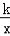 (k>0)于点E、F。
(k>0)于点E、F。
(1)若k=2,m=3,求直线EF的解析式;
(2)O为坐标原点,连接OF,若∠BOF=22.5°,多边形BOAEF的面积是2,求k值。
(1)直线EF解析式为y=﹣x+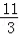 ;(2)k=1 。
;(2)k=1 。
【解析】
试题分析:(1)将k的值代入确定出反比例解析式,将m的值代入确定出M坐标,根据图形得到E的横坐标与F的纵坐标都为3,代入反比例解析式中确定出E与F坐标,设直线EF解析式为y=kx+b,将E与F坐标代入求出k与b的值,即可确定出直线EF的解析式;
(2)连接EF,OM,OE,由M横纵坐标相等得到四边形AOBM为正方形,由正方形的性质及∠BOF=22.5°,得到三角形BOF、三角形FCO、三角形ECO及三角形AOE全等,三角形BOF的面积等于|k|的一半,表示出四个面积之和,即为五边形BOAEF的面积,根据五边形的面积为2列出关于k的方程,求出方程的解即可得到k的值。
试题解析:(1)将k=2,m=3代入得:反比例解析式为y= ,M(3,3),
,M(3,3),
∵MA⊥x轴,MB⊥y轴,
∴E的横坐标为3,F纵坐标为3,
代入反比例解析式得:E(3, ),F(
),F( ,3),
,3),
设直线EF解析式为y=kx+b,
将E与F坐标代入得: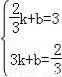 ,
,
解得: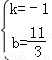 ,
,
则直线EF解析式为y=﹣x+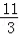 ;
;
(2)连接OM,EF,OE,OM与EF交于点C,
∵M(m,m),反比例解析式为y= ,
,
∴E(m,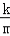 ),F(
),F(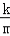 ,m),即E与F关于y=x对称,四边形AOBM为正方形,
,m),即E与F关于y=x对称,四边形AOBM为正方形,
∵∠BOF=22.5°,
∴∠BOF=∠COF=∠EOC=∠AOE=22.5°,
由对称性得到∠FCO=∠ECO=90°,
在△BOF和△AOE中,
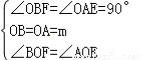 ,
,
∴△BOF≌△AOE(ASA),
同理△BOF≌△COF,△COF≌△AOE,
∴BF=AE=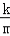 ,
,
又BM=AM=m,
∴S△BOF= m•
m•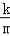 =
= k,
k,
∴S五边形BOAEF=4S△BOF=2k=2,
则k=1。
考点:反比例函数综合题。


科目:初中数学 来源:2013-2014学年辽宁省大石桥市中考模拟考试数学试卷(解析版) 题型:填空题
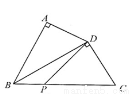
如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为 。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年辽宁省大石桥市中考模拟考试数学试卷(解析版) 题型:选择题
如图是由七个相 同的小正方体摆成的几何体,则这个几何体的俯视图是( )


A. B. C. D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年福建省南平市中考模拟数学试卷(解析版) 题型:填空题
一个圆形转盘被平均分成红、黄、蓝3个扇形区域,向其投掷一枚飞镖,飞镖落在红色区域的概率是 。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖南省长沙市九年级下学期期中考试数学试卷(解析版) 题型:解答题
我市实施新课程改革后,学生的自主学习、合作交流能力有很大提高,张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
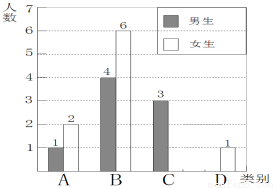
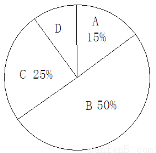
(1)本次调查中,张老师一共调查了 名同学,并将上面的条形统计图补充完整。
(2)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期第一次月考数学试卷(解析版) 题型:选择题
二次函数y=ax2+bx的图象如图所示,那么一次函数y=ax+b的图象大致是( )[来~#源

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com