
【题目】在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图①,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.

【答案】(1)证明见解析;(2)EG=![]() AG﹣BG,理由见解析.
AG﹣BG,理由见解析.
【解析】试题分析:(1)如图,作∠GAH=∠EAB交GE于点H,易证△ABG≌△AEH ,再判定△AGH是等边三角形,即可得结论;(2)EG=![]() AG-BG,如图②,作∠GAH=∠EAB交GE于点H,类比(1)的方法证明△ABG≌△AEH,再判定△AGH是等腰直角三角形,即可得结论.
AG-BG,如图②,作∠GAH=∠EAB交GE于点H,类比(1)的方法证明△ABG≌△AEH,再判定△AGH是等腰直角三角形,即可得结论.
试题解析:
如图,作∠GAH=∠EAB交GE于点H
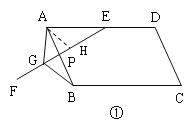
∴∠GAB=∠HAE
∵∠EAB =∠EGB,∠APE=∠BPG
∴∠ABG=∠AEH
又∵AB=AE
∴△ABG≌△AEH
∴BG=EH,AG=AH
∵∠GAH=∠EAB=60°
∴△AGH是等边三角形
∴AG=GH
∴EG=AG+BG
(2) EG=![]() AG-BG,
AG-BG,
如图②,作∠GAH=∠EAB交GE于点H
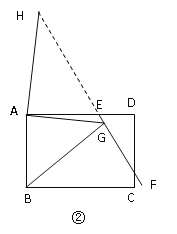
∴∠GAB=∠HAE
又∵∠EGB=∠EAB=90°
∴∠ABG+∠AEG=∠AEG+∠AEH=180°
∴∠ABG=∠AEH
又∵AB=AE
∴△ABG≌△AEH
∴BG=EH,AG=AH
又∵∠GAH =∠EAB=90°
∴△AGH是等腰直角三角形
∴![]() AG=HG
AG=HG
∴EG=![]() AG-BG
AG-BG


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】雷达二维平面定位的主要原理是:测量目标的两个信息―距离和角度,目标的表示方法为![]() ,其中,m表示目标与探测器的距离;
,其中,m表示目标与探测器的距离;![]() 表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为
表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为![]() ,目标C的位置表示为
,目标C的位置表示为![]() .用这种方法表示目标B的位置,正确的是( )
.用这种方法表示目标B的位置,正确的是( )

A. (-4, 150°) B. (4, 150°) C. (-2, 150°) D. (2, 150°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB>BC,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于![]() EF的长半径画弧,两弧交于点G;作射线AG交CD于点H.则下列结论:①AG平分∠DAB,②CH=
EF的长半径画弧,两弧交于点G;作射线AG交CD于点H.则下列结论:①AG平分∠DAB,②CH=![]() DH,③△ADH是等腰三角形,④S△ADH=
DH,③△ADH是等腰三角形,④S△ADH=![]() S四边形ABCH.
S四边形ABCH.
其中正确的有( )

A. ①②③ B. ①③④ C. ②④ D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是__.
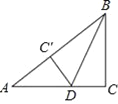
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保护环境,我市公交公司计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com