
 如图,已知△ABC中,点D、E分别在边AB和AC上,DE∥BC,点F是DE延长线上的点,$\frac{AD}{BD}=\frac{DE}{EF}$,联结FC,若$\frac{AE}{AC}=\frac{2}{3}$,求$\frac{AD}{FC}$的值.
如图,已知△ABC中,点D、E分别在边AB和AC上,DE∥BC,点F是DE延长线上的点,$\frac{AD}{BD}=\frac{DE}{EF}$,联结FC,若$\frac{AE}{AC}=\frac{2}{3}$,求$\frac{AD}{FC}$的值. 分析 由平行线分线段成比例定理和已知条件得出$\frac{AE}{EC}=\frac{DE}{EF}$,证出AB∥CF,再由平行线分线段成比例定理和比例的性质即可得出结果.
解答 解:∵DE∥BC,
∴$\frac{AD}{BD}=\frac{AE}{EC}$,
又∵$\frac{AD}{BD}=\frac{DE}{EF}$,
∴$\frac{AE}{EC}=\frac{DE}{EF}$,
∴AB∥CF,
∴$\frac{AD}{FC}$=$\frac{AE}{EC}$,
∵$\frac{AE}{AC}=\frac{2}{3}$,
∴$\frac{AE}{EC}=\frac{2}{1}$=2,
∴$\frac{AD}{FC}$=2.
点评 本题考查了平行线分线段成比例定理以及逆定理;熟练掌握平行线分线段成比例定理,证明AB∥CF是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图(1),一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在线段OP上滑动,将窗户OM按图示方向向内旋转45°到达ON位置,如图(2),此时,点A、C的对应位置分别是点B、D,测量出∠ODB为37°,点D到点O的距离为28cm.
如图(1),一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在线段OP上滑动,将窗户OM按图示方向向内旋转45°到达ON位置,如图(2),此时,点A、C的对应位置分别是点B、D,测量出∠ODB为37°,点D到点O的距离为28cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
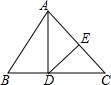 如图,在△ABC中,AD是高,DE是AC的垂直平分线,AE=4cm,△ABD的周长为15cm,则△ABC的周长为( )
如图,在△ABC中,AD是高,DE是AC的垂直平分线,AE=4cm,△ABD的周长为15cm,则△ABC的周长为( )| A. | (23+4$\sqrt{2}$)cm | B. | 23cm | C. | 19cm | D. | 11cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AD,AE分别是△ABC的高和角平分线.
如图,AD,AE分别是△ABC的高和角平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是某个大型商场的自动扶梯侧面示意图,已知自动扶梯AC的坡度为1:2,AC的长度为5$\sqrt{5}$米,AB为底楼地面,CD为二楼侧面,EF为二楼楼顶,当然有EF∥AB∥CD,E为自动扶梯AC的最高端C的正上方,过C的直线EG⊥AB于G,在自动扶梯的底端A测得E的仰角为42°,求该商场二楼的楼高CE.
如图是某个大型商场的自动扶梯侧面示意图,已知自动扶梯AC的坡度为1:2,AC的长度为5$\sqrt{5}$米,AB为底楼地面,CD为二楼侧面,EF为二楼楼顶,当然有EF∥AB∥CD,E为自动扶梯AC的最高端C的正上方,过C的直线EG⊥AB于G,在自动扶梯的底端A测得E的仰角为42°,求该商场二楼的楼高CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com