
分析 利用“获利1000元”,即销售额-进价=利润,作为相等关系列方程,解方程求解后要代入实际问题中检验是否符合题意,进行值的取舍.
解答 解:设第一个月单价降低x元时,销售完这批T恤获得的利润为1000元.
根据题意得-10x2+100x+1000=1000.
解这个方程,得x1=0,x2=10.
从增加销售量的角度看,取x=10.
则70-10=60(元)
答:第一个月该商店售价为60元时,销售完这批T恤获得的利润为1000元.
点评 此题主要考查了二次函数的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.有关销售问题中的等量关系一般为:利润=售价-进价.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
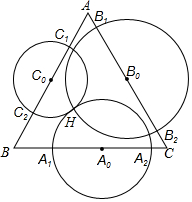 已知H是锐角△ABC的垂心,以边BC的中点为圆心、过点H的圆与直线BC交于A1,A2两点,以边CA的中点为圆心、过点H的圆与直线CA交于B1、B2两点,以边AB的中点为圆心、过点H的圆与直线AB交于C1、C2两点,证明:A1,A2,B1,B2,C1,C2六点共圆.
已知H是锐角△ABC的垂心,以边BC的中点为圆心、过点H的圆与直线BC交于A1,A2两点,以边CA的中点为圆心、过点H的圆与直线CA交于B1、B2两点,以边AB的中点为圆心、过点H的圆与直线AB交于C1、C2两点,证明:A1,A2,B1,B2,C1,C2六点共圆.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
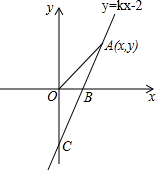 如图,直线y=kx-2与x轴,y轴分别交于B,C两点,其中OB=1.
如图,直线y=kx-2与x轴,y轴分别交于B,C两点,其中OB=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(a,b),点F在AB边上,将矩形沿OF翻折,使点A落在点D处,DF与OC交于点E,且OE平分∠FOD,若a,b是一元二次方程x2-9x+18=0的两个根(a>b),解答下列问题:
如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(a,b),点F在AB边上,将矩形沿OF翻折,使点A落在点D处,DF与OC交于点E,且OE平分∠FOD,若a,b是一元二次方程x2-9x+18=0的两个根(a>b),解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
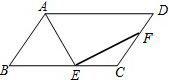 如图,平行四边形ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,EC=CF,若BC=7,DF=3,tan∠AEB=3,则平行四边形ABCD的面积为21.
如图,平行四边形ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,EC=CF,若BC=7,DF=3,tan∠AEB=3,则平行四边形ABCD的面积为21.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com