Question

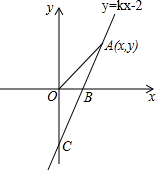
9．如图，直线y=kx-2与x轴，y轴分别交于B，C两点，其中OB=1．
（1）求k的值；
（2）若点A（x，y）是第一象限内的直线y=kx-2上的一个动点，当点A运动过程中，试写出△AOB的面积S与x的函数关系式；
（3）探索：
①当点A运动到什么位置时，△AOB的面积是1；
②在①成立的情况下，x轴上是否存在一点P，使△POA是等腰三角形？若存在，请写出满足条件的所有P点的坐标；若不存在，请说明理由．

Answer 1

分析 （1）先确定出点B的坐标，代入函数解析式中即可求出k；
（2）借助（1）得出的函数关系式，利用三角形的面积公式即可求出函数关系式；
（3）①利用三角形的面积求出求出点A坐标；
②设出点P（m，0），表示出AP，OP，计算出OA，分三种情况讨论计算即可得出点P坐标．

解答 解：（1）∵OB=1，
∴B（1，0），
∵点B在直线y=kx-2上，
∴k-2=0，
∴k=2
（2）由（1）知，k=2，
∴直线BC解析式为y=2x-2，
∵点A（x，y）是第一象限内的直线y=2x-2上的一个动点，
∴y=2x-2（x＞1），
∴S=S_△AOB=$\frac{1}{2}$×OB×|y_A|=$\frac{1}{2}$×1×|2x-2|=x-1，
（3）①如图，

由（2）知，S=x-1，
∵△AOB的面积是1；
∴x=2，
∴A（2，2），
∴OA=2$\sqrt{2}$，
②设点P（m，0），
∵A（2，2），
∴OP=|m|，AP=$\sqrt{（2-m）^{2}+4}$，
①当OA=OP时，∴2$\sqrt{2}$=|m|，∴m=±2$\sqrt{2}$，∴P₁（-2$\sqrt{2}$，0），P₂（2$\sqrt{2}$，0），
②当OA=AP时，∴2$\sqrt{2}$=$\sqrt{（2-m）^{2}+4}$，∴m=0或m=4，∴P₃（4，0），
③当OP=AP时，∴|m|=$\sqrt{（2-m）^{2}+4}$，∴m=2，∴P₄（2，0），
即：满足条件的所有P点的坐标为P₁（-2$\sqrt{2}$，0），P₂（2$\sqrt{2}$，0），P₃（4，0），P₄（2，0）．

点评 此题是一次函数综合题，主要考查了待定系数法，三角形的面积公式，等腰三角形的性质，解本题的关键是求出点A的坐标．