练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．李丽上星期六买进某公司股票1000股，每股27元，如表为本周内每日该股票的涨跌情况（单位：元）
    星  期一二三四五
    每股涨跌（元）+4+4.5-1-2.5+2
    （1）星期三收盘时，每股是多少元？
    （2）本周内的最高价每股是多少元？最低价每股是多少元？
    （3）已知李丽买进股票时付1.5‰的手续费，卖出时需付1.5‰成交费的手续费和1‰的交易费，如果她在星期六收盘时全部卖出，她的收益情况如何？

    分析 （1）根据表格中的数据确定出星期三收盘时每股的价钱即可；
    （2）根据表格确定出5天的收盘价，即可确定出最高价与最低价；
    （3）根据买进与卖出的手续费与交易费，确定出星期六收盘时全部卖出时的收益．

    解答 解：（1）根据题意得：27+4+4.5-1=34.5（元）；
    （2）根据题意得：5天的收盘价分别是31元、35.5元、34.5元、32元、34元，
    则本周内的最高价每股是35.5元；最低价每股31元．
    （3）根据题意得：34×1000-34×1000×（1.5‰+1‰）-27×1000-27×1000×1.5‰=6874.5（元），
    则他的收益是6874.5元．

    点评 此题考查了正数与负数，弄清题中的数据是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．一台电视机的成本为a元，销售价比成本价增加25%，因库存积压，所以按销售价的70%出售，那么每台实际售价为多少元？若这种电视机成本价为3000元，那么每台实际售价为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．方程5x2=$\sqrt{2}$x的二次项系数是5，一次项系数是-$\sqrt{2}$，常数项是0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图1，在平面直角坐标系中，∠BAO与∠ABO的角平分线相交于点I．
    （1）求∠AIB的度数；
    （2）如图2，过I作IC⊥OB于点C，求证：AB-AO+BO=2BC．
    （3）如图3，D为x轴正半轴上一动点，作△BID关于DI的对称图形△B′ID，B′D交AB于点E，交y轴于点F，若AO=6，BO=8，则下列结论中：①△AEF的周长是定值；②△AEF的面积是定值，其中有且只有一个结论是正确的，请指出正确的结论并求其值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．用适当的方法解下列方程：
    （1）3（x-1）2-27=0                  
    （2）3x2=6x
    （3）4x2-8x+1=0                    
    （4）-2x2+5x-2=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．先化简，再求值：x2-3（2x2-xy）+2（xy-x2），其中|x+3|+（y-2）2=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．计算
    （1）（-8）+47+8+（-27）
    （2）-2-（-4）-（+5）+（-8）-（-9）
    （3）|-4|+|-5|-|（-$\frac{1}{2}$）+（-0.5）|
    （4）（-0.25）×0.5×（-$\frac{2}{7}$）×4
    （5）（-36）×（$\frac{4}{9}$-$\frac{5}{6}$+1$\frac{1}{3}$）
    （6）5÷$\frac{2}{3}$×$\frac{3}{2}$×（-$\frac{1}{5}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

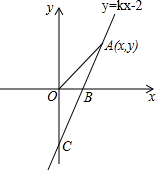    9．如图，直线y=kx-2与x轴，y轴分别交于B，C两点，其中OB=1．
    （1）求k的值；
    （2）若点A（x，y）是第一象限内的直线y=kx-2上的一个动点，当点A运动过程中，试写出△AOB的面积S与x的函数关系式；
    （3）探索：
    ①当点A运动到什么位置时，△AOB的面积是1；
    ②在①成立的情况下，x轴上是否存在一点P，使△POA是等腰三角形？若存在，请写出满足条件的所有P点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

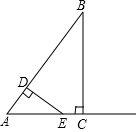    10．如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，动点D从点A出发以每秒3个单位的速度运动至点B，过点D作DE⊥AB交射线AC于点E．设点D的运动时间为t秒（t＞0）．
    （1）线段AE的长为5t．（用含t的代数式表示）
    （2）若△ADE与△ACB的面积比为1：4时，求t的值．
    （3）设△ADE与△ACB重叠部分图形的周长为L，求L与t之间的函数关系式．
    （4）当直线DE把△ACB分成的两部分图形中有一个是轴对称图形时，直接写出t的值．

    查看答案和解析>>

    同步练习册答案