
【题目】如图,已知∠ADC=∠EFC,∠3=∠C,可推得∠1=∠2.理由如下:
解:因为∠ADC=∠EFC(已知)
所以AD∥EF( ).
所以∠1=∠4( ),
因为∠3=∠C(已知),
所以AC∥DG( ).
所以∠2=∠4( ).
所以∠1=∠2(等量代换).

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】小明和小英在周末和爸爸妈妈以及爷爷奶奶一行6人,自驾外出旅游,出发前油箱里有油5升,在加油站加140元的油.已知油价是7元/升,目的地距离出发地320千米,正常行驶时,车子的耗油情况是0.42元/千米.
(1)在加油站加油 升;车子的耗油情况换算成 升/千米.
(2)在行驶过程中,设油箱内余油y(升),行驶路程x(千米),将y表示为x的函数.
(3)若油箱里余油量低于5升会自动报警,通过计算回答,小明他们在到达目的地之前,车子是否会自动报警.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD.
(1)求证:DB=DE;
(2)过点D作DF垂直BE,垂足为F,若CF=3,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
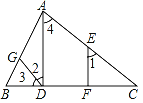
【题目】如图,已知∠ADC=∠EFC,∠3=∠C,可推得∠1=∠2.理由如下:
解:因为∠ADC=∠EFC(已知)
所以AD∥EF( ).
所以∠1=∠4( ),
因为∠3=∠C(已知),
所以AC∥DG( ).
所以∠2=∠4( ).
所以∠1=∠2(等量代换).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2﹣2ax+c(a<0)的图象与x轴负半轴交于点A(﹣1,0),与y轴正半轴交于点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过A、B.
(1)求一次函数解析式;
(2)求顶点P的坐标;
(3)平移直线AB使其过点P,如果点M在平移后的直线上,且 ![]() ,求点M坐标;
,求点M坐标;
(4)设抛物线的对称轴交x轴于点E,连接AP交y轴于点D,若点Q、N分别为两线段PE、PD上的动点,连接QD、QN,请直接写出QD+QN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某面粉加工厂要加工一批小麦,2台大面粉机和5台小面粉机同时工作2小时共加工小麦1.1万斤;3台大面粉机和2台小面粉机同时工作5小时共加工小麦3.3万斤.
(1)1台大面粉机和1台小面粉机每小时各加工小麦多少万斤?
(2)该厂现有9.45万斤小麦需要加工,计划使用8台大面粉机和10台小面粉机同时工作5小时,能否全部加工完?请你帮忙计算一下.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AC为斜边作Rt△ADC,使∠ADC=90°,∠CAD=∠CAB=26°,E、F分别是BC、AC的中点,则∠EDF等于°. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com