(1)阅读填空:
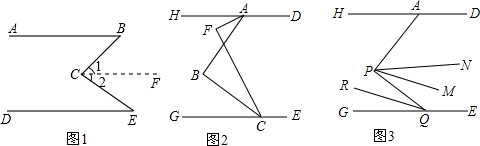
如图1,AB∥DE,试问∠B、∠E、∠BCE有什么关系.
解:∠B+∠E=∠BCE
过点C作CF∥AB,
则∠B=∠1【
】
又∵AB∥DE,AB∥CF,
∴CF∥DE
∴∠E=∠2【
】
∴∠B+∠E=∠1+∠2,即∠B+∠E=∠BCE.
(2)应用解答:
观察上面图形与结论,解决下面的问题:
如图2,∠DAB+∠B+∠BCE=360°,作∠BCF=∠BCG,CF与∠BAH的平分线交于F,若∠F的余角等于2∠B的补角,求∠BAH的度数.
(3)拓展深化:
如图3,在前面的条件下,若点P是AB上一点,Q是GE上任一点,QR平分∠PQR,PM∥QR,PN平分∠APQ,下列结论:①∠APQ+∠NPM的值不变;②∠NPM的度数不变,可以证明,只有一个是正确的,请你做出正确的选择并求值.

