Question

3．已知A点坐标为（-2，0），B点坐标为（8，0），且△ABC为等边三角形．
（1）求C点坐标；
（2）求△ABC的周长和面积．

Answer 1

分析 （1）根据已知条件画出草图结合等边三角形的性质分析C点的可能位置，分情况求解；
（2）根据等边三角形的周长和面积解答即可．

解答 解：∵A点坐标为（-2，0），B点坐标为（8，0），
∴AB=10，以点A和B为圆心，10为半径画弧，交于点C₁，C₂，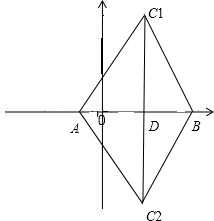
，
（1）∵AB=10，
∴AD=5，AC₁=10，
在Rt△AC₁D中，${C}_{1}D=\sqrt{A{{C}_{1}}^{2}-A{D}^{2}}=\sqrt{1{0}^{2}-{5}^{2}}=5\sqrt{3}$，
∴${C}_{1}（3，5\sqrt{3}），{C}_{2}（3，-5\sqrt{3}）$；
（2）∵AB=10，
∴△ABC的周长=3×10=30，
∴△ABC的面积=$\frac{1}{2}AB•CD=\frac{1}{2}×10×5\sqrt{3}=25\sqrt{3}$．

点评 此题考查等边三角形的性质，关键是根据已知条件画出草图结合等边三角形的性质分析C点的可能位置．