
【题目】解答题
(1)求不等式组  的解集;
的解集;
(2)如图,在△ABC中,己知∠ABC=30°,将△ABC绕点B逆时针旋转50°后得到△A′BC′,已知A′C′∥BC,求∠A的度数. 
【答案】
(1)解: 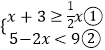 ,
,
∵解不等式①得:x≥﹣6,
解不等式②得:x>﹣2,
∴不等式组的解集为x>﹣2
(2)解:∵将△ABC绕点B逆时针旋转50°后得到△A′BC′,
∠A′BA=50°,
∵∠ABC=30°,
∴∠A′BC=80°,
∵A′C′∥BC,
∴∠A′+∠A′BC=180°,
∴∠A′=100°,
∴根据旋转得出∠A=∠A′=100°
【解析】(1)求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可;(2)求出∠A′BC,根据平行线的性质求出∠A′,根据旋转的性质得出即可.
【考点精析】本题主要考查了一元一次不等式组的解法和平行线的性质的相关知识点,需要掌握解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 );两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能正确解答此题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(1)请判断:AF与BE的数量关系是______________.位置关系是_______________.
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请做出判断并给与证明.


(图1) (图2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个两位数,十位上数字是x,个位上数字是y,若把十位上数字和个位上数字对调,所得的两位数是 ( )
A. yx B. y+x C. 10y+x D. 10x+y
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在图①中以P为顶点画∠P,使∠P的两边分别和∠1的两边垂直;
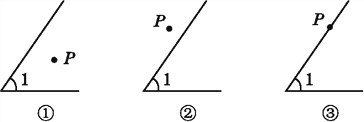
(2)量一量∠P和∠1的度数,它们之间的数量关系是 ;
(3)同样在图②和图③中以P为顶点作∠APB,使∠APB的两边分别和∠1的两边垂直,分别写出图②和图③中∠APB和∠1之间的数量关系(不要求写出理由).
图②: ,
图③: ;
(4)由上述三种情形可以得到一个结论:如果一个角的两边分别和另一个角的两边垂直,那么这两个角 (不要求写出理由).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com