
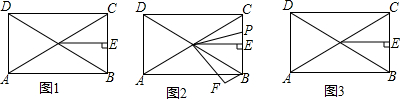
���� ��1���ɡ�ABC=90�㣬��BAC=30��õ���ACB=60�㣬����ֱ��������б�����������ʵõ�OB=OC������жϡ�OCBΪ�ȱ������Σ�����OE��BC��OE=$\frac{\sqrt{3}}{2}$BC��
��2��������ת�����ʵõ���POF=60�㣬OP=OF���á�COP=��BOF����ɸ��ݡ�SAS�����жϡ�OCP�ա�OBF����CP=BF������CP=BC-BPODE=$\frac{\sqrt{3}}{2}$BC�ɵõ�BF+BP=$\frac{2\sqrt{3}}{3}$OE��
��3���루2����֤������һ���õ���DCP�ա�DBF�õ�CP=BF��Ȼ��ֵ�P���߶�BC�ӳ�����һ������P���߶�CB�ӳ�����һ���㣬���ǵõ����ۣ�
��� �⣺��1���ߡ�ABC=90�㣬��BAC=30�㣬
���ACB=60�㣬
�ߵ�O��AC���е㣬
��OB=OC��
���OCBΪ�ȱ������Σ�
��OE��BC��
��OE=$\frac{\sqrt{3}}{2}$BC��
�ʴ�Ϊ��DE=$\frac{\sqrt{3}}{2}$BC��
��2����ͼ2�� BF+BP=$\frac{2\sqrt{3}}{3}$DE���������£�
BF+BP=$\frac{2\sqrt{3}}{3}$DE���������£�
���߶�OP�Ƶ�O˳ʱ����ת60�㣬�õ��߶�OF��
���POF=60�㣬OP=OF��
����COB=60�㣬
���COB-��POB=��POF-��POB��
���COP=��BOF��
�ڡ�OCP�͡�OBF�У�
$\left\{\begin{array}{l}{OC=OB}\\{��COP=��BOF}\\{OP=OF}\end{array}\right.$��
���OCP�ա�OBF��SAS����
��CP=BF��
��CP=BC-BP��
��BF+BP=BC��
��OE=$\frac{\sqrt{3}}{2}$BC��
��BC=$\frac{2\sqrt{3}}{3}$OE��
��BF+BP=$\frac{2\sqrt{3}}{3}$OE�� ��3����ͼ3��
��3����ͼ3��
��P���߶�BC�ӳ�����һ���㣬
�루2��һ����֤����OCP�ա�OBF��
��CP=BF��
��CP=BP-BC��
��BP-BF=BC��
��BP-BF=$\frac{2\sqrt{3}}{3}$OE���� ��ͼ4����P���߶�CB�ӳ�����һ�����루2��һ����֤����OCP�ա�OBF��
��ͼ4����P���߶�CB�ӳ�����һ�����루2��һ����֤����OCP�ա�OBF��
��CP=BF��
��CP=BP+BC��
��BF-BP=BC��
��BF-BP=$\frac{2\sqrt{3}}{3}$OE��
���� ���⿼���˾��ε����ʣ�ȫ�������ε��ж������ʣ�Ҳ�����˵ȱ������ε��ж��������Լ���30�ȵ�ֱ�����������ߵĹ�ϵ����ȷ������ͼ���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
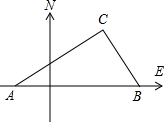 ��ͼ�����ҹ��غ���һ�Ҳ����������ִ������ҹ������Һ����ס�������Ѳ��ͧ���������13�����A��B��������ǰȥ���أ������Ӻ�ͬʱ����C�ؽ������أ���֪��Ѳ��ͧÿСʱ����120�����Ѳ��ͧÿСʱ����50�����Ѳ��ͧ�ĺ���Ϊ��ƫ��40�㣮
��ͼ�����ҹ��غ���һ�Ҳ����������ִ������ҹ������Һ����ס�������Ѳ��ͧ���������13�����A��B��������ǰȥ���أ������Ӻ�ͬʱ����C�ؽ������أ���֪��Ѳ��ͧÿСʱ����120�����Ѳ��ͧÿСʱ����50�����Ѳ��ͧ�ĺ���Ϊ��ƫ��40�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6�� | B�� | 7�� | C�� | 8�� | D�� | 9�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
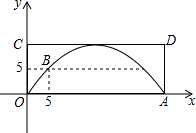
 ��ͼ����ƽ��ֱ������ϵxOy�У����κ���y=$\frac{1}{3}{x^2}$+bx+c��ͼ����y�ύ�ڵ�A����˫����y=$\frac{8}{x}$��һ��������B�����ĺ�����Ϊ4������B��ֱ��l��x�ᣬ��ö��κ���ͼ������һ����C��ֱ��AC��y���ϵĽؾ���-6��
��ͼ����ƽ��ֱ������ϵxOy�У����κ���y=$\frac{1}{3}{x^2}$+bx+c��ͼ����y�ύ�ڵ�A����˫����y=$\frac{8}{x}$��һ��������B�����ĺ�����Ϊ4������B��ֱ��l��x�ᣬ��ö��κ���ͼ������һ����C��ֱ��AC��y���ϵĽؾ���-6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��һ�����������ţ�����CD��ˮ��ƽ�У�������ˮλʱ����ˮ���OAΪ30�ף�����B��Ϊ����ˮλ��ʶ����B��OC��ˮƽ���������ˮ��OA�ľ��붼Ϊ5�ף�
��ͼ��һ�����������ţ�����CD��ˮ��ƽ�У�������ˮλʱ����ˮ���OAΪ30�ף�����B��Ϊ����ˮλ��ʶ����B��OC��ˮƽ���������ˮ��OA�ľ��붼Ϊ5�ף��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com