
分析 根据x是m的立方根可得a+b=3,由y是x的相反数得b-6=-m,结合m=3a-7联立方程组求得a、b、m的值,进而可得x、y,列式计算可得答案.
解答 解:依题意,得 $\left\{\begin{array}{l}{a+b=3}\\{b-6=-m}\\{m=3a-7}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=5}\\{b=-2}\\{m=8}\end{array}\right.$,
则x=$\root{3}{8}$=2,y=$\root{3}{-2-6}$=-2.
则 $\root{3}{{x}^{2}+{y}^{2}}$=$\root{3}{{2}^{2}+(-2)^{2}}$=$\root{3}{8}$=2.
点评 本题考查了立方根的定义、相反数及解方程组的能力,正确理解定义,求得x,y的值是关键.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:解答题
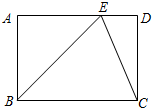 如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
如图,在矩形ABCD中,点E在AD上,EC平分∠BED.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
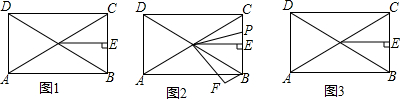
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
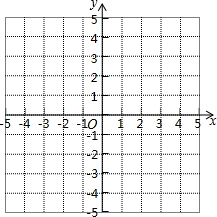 设k≠0,若函数y1=(x-k)2+2k和y2=-(x+k)2-2k的图象与y轴依次交于A,B两点,函数y1,y2的图象的顶点分别为C,D.
设k≠0,若函数y1=(x-k)2+2k和y2=-(x+k)2-2k的图象与y轴依次交于A,B两点,函数y1,y2的图象的顶点分别为C,D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
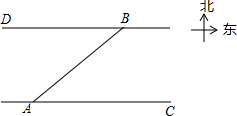 如图,一艘客轮以30km/h的速度由A码头出发沿北偏东53°方向航行至B码头,已知A、B两码头所在的河岸均为东西走向,河宽为16km,求该客轮至少用多长时间才能到达B码头?
如图,一艘客轮以30km/h的速度由A码头出发沿北偏东53°方向航行至B码头,已知A、B两码头所在的河岸均为东西走向,河宽为16km,求该客轮至少用多长时间才能到达B码头?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com