
分析 连接QM,MP,PN,PQ,过N作NE⊥AB于E,过Q作QF⊥BC于F,得到四边形BCNE,四边形CDQF是矩形,根据矩形的性质得到EN=BC,QF=CD,根据正方形的性质得到AB=BC=CD=AD,证得NE=QF,通过全等三角形的性质得到MN=PQ;根据已知条件得到Rt△PQF≌Rt△MNE,由全等三角形的性质得到∠PQF=∠MNE,根据余角的性质即可得到MN⊥PQ;根据全等三角形的性质得到AM=CN,PC=AQ,由线段的和差得到PB=QD,BM=DN,于是得到△BMP≌△DNQ,由△AMQ∽△CNP和已知条件推不出△BMP∽△DNQ的条件.
解答 解:连接QM,MP,PN,PQ,过N作NE⊥AB于E,过Q作QF⊥BC于F,
则四边形BCNE,四边形CDQF是矩形,
∴EN=BC,QF=CD,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,
∴NE=QF,
①∵MN⊥PQ,
∴∠PQF=∠MNE,
在△PQF与△MNE中,$\left\{\begin{array}{l}{∠PQF=∠ENM}\\{QF=MN}\\{∠QFP=∠NEM}\end{array}\right.$,
∴△PQF≌△MNE,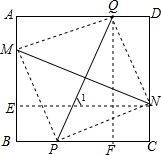
∴MN=PQ;
②在Rt△PQF与Rt△MNE中,$\left\{\begin{array}{l}{QF=NE}\\{PQ=MN}\\{\;}\end{array}\right.$,
∴Rt△PQF≌Rt△MNE,
∴∠PQF=∠MNE,
∵∠PQF+∠1=90°,
∴∠MNE+∠1=90°,
∴MN⊥PQ;
③∵△AMQ≌△CNP,
∴AM=CN,PC=AQ,
∴PB=QD,BM=DN,
在△BMP与△DNQ中,$\left\{\begin{array}{l}{BM=DN}\\{∠B=∠D}\\{PB=DQ}\end{array}\right.$,
∴△BMP≌△DNQ,
④由△AMQ∽△CNP和已知条件推不出△BMP∽△DNQ的条件.
故答案为:①②③.
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,正方形的性质,正确的作出辅助线构造全等三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
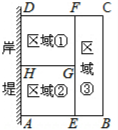 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块长方形区域,而且这三块长方形区域的面积相等.设BC的长度为xm,AB为ym.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块长方形区域,而且这三块长方形区域的面积相等.设BC的长度为xm,AB为ym.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com