
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用三角形的外心的定义、两圆的位置关系、实数的性质分别判断后即可确定正确的选项.
解答 解:①三角形的外心是三角形三边垂直平分线的交点,故正确;
②16-4×(1-a)×6=16-24+24a=24a-8=0,
解得,a=$\frac{1}{3}$,
函数y=(1-a)x2-4x+6与x轴只有一个交点,则a=$\frac{1}{3}$,故正确;
③半径分别为1和2的两圆相切,则圆心距为3或1,故错误;
④若对于任意x>1的实数,都有ax>1成立,则a不一定≥1,故错误.
故选:B.
点评 本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.


科目:初中数学 来源: 题型:解答题
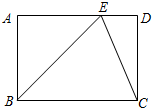 如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
如图,在矩形ABCD中,点E在AD上,EC平分∠BED.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 设k≠0,若函数y1=(x-k)2+2k和y2=-(x+k)2-2k的图象与y轴依次交于A,B两点,函数y1,y2的图象的顶点分别为C,D.
设k≠0,若函数y1=(x-k)2+2k和y2=-(x+k)2-2k的图象与y轴依次交于A,B两点,函数y1,y2的图象的顶点分别为C,D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
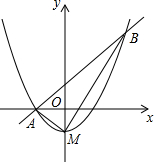 如图,顶点M(0,-1)在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,连结AM,BM.
如图,顶点M(0,-1)在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,连结AM,BM.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某同学在距电视塔BC塔底水平距离200米的A处,看塔顶C的仰角为20°(不考虑身高因素),则此塔BC的高约为( )
某同学在距电视塔BC塔底水平距离200米的A处,看塔顶C的仰角为20°(不考虑身高因素),则此塔BC的高约为( )| A. | 68米 | B. | 73米 | C. | 127米 | D. | 188米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
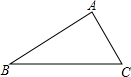 已知:如图△ABC,∠ACB=2∠B=60°,BC=4.请按要求进行尺规作图,作∠ACB的平分线交AB于点D,再过点D作DE⊥BC,垂足为E,并求出AD的长.(不写作法,保留作图痕迹).
已知:如图△ABC,∠ACB=2∠B=60°,BC=4.请按要求进行尺规作图,作∠ACB的平分线交AB于点D,再过点D作DE⊥BC,垂足为E,并求出AD的长.(不写作法,保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
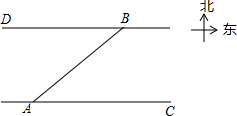 如图,一艘客轮以30km/h的速度由A码头出发沿北偏东53°方向航行至B码头,已知A、B两码头所在的河岸均为东西走向,河宽为16km,求该客轮至少用多长时间才能到达B码头?
如图,一艘客轮以30km/h的速度由A码头出发沿北偏东53°方向航行至B码头,已知A、B两码头所在的河岸均为东西走向,河宽为16km,求该客轮至少用多长时间才能到达B码头?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组:$\left\{\begin{array}{l}{3(x-2)≤x-4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$并将其解集表示在如图所示的数轴上.
解不等式组:$\left\{\begin{array}{l}{3(x-2)≤x-4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$并将其解集表示在如图所示的数轴上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com