练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．某同学在距电视塔BC塔底水平距离200米的A处，看塔顶C的仰角为20°（不考虑身高因素），则此塔BC的高约为（　　）
    （参考数据：sin20°≈0.3420，cos20°≈0.9397，tan20°≈0.3640）（保留到个位）
    A．68米B．73米C．127米D．188米

    分析 在RT△ABC中，由tanA=$\frac{BC}{AB}$可得BC=AB•tanA，代入计算即可．

    解答 解：在RT△ABC中，∵∠A=20°，AB=200，tanA=$\frac{BC}{AB}$
    ∴BC=AB•tanA≈200×0.3640≈73米，
    故选：B．

    点评 本题主要考查解直角三角形中仰角俯角问题，熟练掌握三角函数的定义是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    16．计算：$\sqrt{18}$+$\sqrt{3}$-3$\sqrt{\frac{1}{3}}$-$\sqrt{8}$-$\frac{1}{5}$$\sqrt{50}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．有若干个数据，最大值是124，最小值是103．用频数分布表描述这组数据时，若取组距为3，则应分为（　　）
    A．6组B．7组C．8组D．9组

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

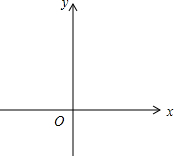    14．如图，在平面直角坐标系xOy中，二次函数y=$\frac{1}{3}{x^2}$+bx+c的图象与y轴交于点A，与双曲线y=$\frac{8}{x}$有一个公共点B，它的横坐标为4，过点B作直线l∥x轴，与该二次函数图象交于另一个点C，直线AC在y轴上的截距是-6．
    （1）求二次函数的解析式；
    （2）求直线AC的表达式；
    （3）平面内是否存在点D，使A、B、C、D为顶点的四边形是等腰梯形？如果存在，求出点D坐标；如果不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列命题中，
    ①三角形的外心是三角形三边垂直平分线的交点；
    ②函数y=（1-a）x2-4x+6与x轴只有一个交点，则a=$\frac{1}{3}$；
    ③半径分别为1和2的两圆相切，则圆心距为3；
    ④若对于任意x＞1的实数，都有ax＞1成立，则a≥1．
    其中正确的个数有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，在△ABC中，点A，B分别在x轴的正、负半轴上（其中OA＜OB），点C在y轴的正半轴上，AB=10，OC=4，∠ABC=∠ACO．
    （1）求经过A，B，C三点的抛物线的函数表达式；
    （2）点D的坐标为（-4，0），P是该抛物线上的一个动点．
    ①直线DP交直线BC于点E，当△BDE是等腰三角形时，直接写出此时点E的坐标；
    ②连结CD，CP，若∠PCD=∠CBD，请求出点P的坐标．

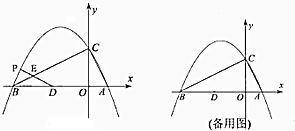
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．为了估计水塘中的鱼数，养鱼者首先从鱼塘中捕获20条鱼，在每条鱼身上做好记号后，把这些鱼放归鱼塘．再从鱼塘中打捞100条鱼，如果在这100条鱼中有5条鱼是有记号的，则估计该鱼塘中的鱼数约为（　　）
    A．300条B．380条C．400条D．420条

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

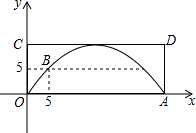    15．如图，一座抛物线型拱桥，桥面CD与水面平行，在正常水位时桥下水面宽OA为30米，拱桥B处为警戒水位标识，点B到OC的水平距离和它到水面OA的距离都为5米．
    （1）按如图所示的直角坐标系，求该抛物线的函数表达式；
    （2）求在正常水位时桥面CD距离水面的高度；
    （3）一货船载长方体货箱高出水面2米（船高不计）．若要使货船在警戒水位时能安全通过该拱桥，则货箱最宽应为多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知Rt△ABC中，∠BAC=90°，AB=AC，△CDE的边CE在射线AC上，CE＜AC，∠DCE=90°，CD=CA，沿CA方向平移△CDE，使点C移动到点A，得到△ABF，过点F作FG⊥BC，垂足为点G，连接EG，DG．
    （1）如图1，边CE在线段AC上，求证：GC=GF；
    （2）在以下A，B两题中任选一题解答，我选择A题．
    A．在图1中，求证：△EFG≌△DCG；
    B．如图2，边CE在线段AC的延长线上，其余条件不变．
    ①在图2中，求证：△EFG≌△DCG；
    ②若∠CDE=20°，直接写出∠CGE的度数．

    查看答案和解析>>

    同步练习册答案