
分析 (1)根据等腰直角三角形的性质和平移的性质即可组织三角形全等的条件;
(2)与(1)类似,运用等腰直角三角形的性质和平移的性质组织全等的条件.
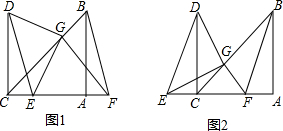
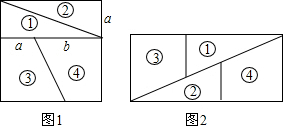
解答 证明:(1)如图1,
∵Rt△ABC中,∠BAC=90°,AB=AC,
∴∠ACB=∠ABC=45°,
∵FG⊥CG,
∴∠FGC=90°,
∴∠GCF+∠GFC=90°,
∴∠GCF=45°=∠GCF,
∴GC=GF,
∵∠DCE=90°
∴∠DCG=90°-45°=45°
∴∠DCG=∠GCF,
∵平移△CDE,得到△ABF,
∴CA=EF,
∵CD=CA,
∴CD=EF,
在△EFG和△DCG中,
$\left\{\begin{array}{l}{EF=DG}\\{∠EFG=∠DCG}\\{GF=GC}\end{array}\right.$,
∴△EFG≌△DCG;
(2)①如图2, 与(1)同理可证:GC=GF,∠GCF=∠GFC=45°
与(1)同理可证:GC=GF,∠GCF=∠GFC=45°
∵∠DCE=90°,
∴∠DCF=90°
∴∠DCG=90°-∠GCF=45°
∴∠DCG=∠GFC
∵△ABF由△CDE平移得到,
∴EC=FA
∴EF=CA
∵AC=CD
∴EF=CD
在△EFG和△DCG中,
$\left\{\begin{array}{l}{EF=CD}\\{∠EFG=∠DCG}\\{GF=GC}\end{array}\right.$,
∴△EFG≌△DCG.
②∠CGE=20°.(设CD交EG于O,只要证明△DOE∽△GOC即可)
点评 此题主要考查三角形全等的证明,认真观察图形,结合已知(等腰直角三角形和平移)组织三角形全等的条件是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 某同学在距电视塔BC塔底水平距离200米的A处,看塔顶C的仰角为20°(不考虑身高因素),则此塔BC的高约为( )
某同学在距电视塔BC塔底水平距离200米的A处,看塔顶C的仰角为20°(不考虑身高因素),则此塔BC的高约为( )| A. | 68米 | B. | 73米 | C. | 127米 | D. | 188米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
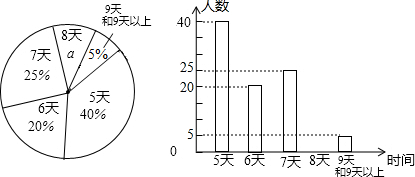
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
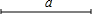 用圆规、直尺作图,不写作法,但要保留作图痕迹.
用圆规、直尺作图,不写作法,但要保留作图痕迹.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组:$\left\{\begin{array}{l}{3(x-2)≤x-4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$并将其解集表示在如图所示的数轴上.
解不等式组:$\left\{\begin{array}{l}{3(x-2)≤x-4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$并将其解集表示在如图所示的数轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
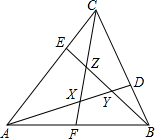 如图,△ABC中,D,E,F分别足BC,CA,AB边上的点,BD:DC=1:2,CE:EA=1:3,AF:FB=1:1,AD,BE,CF围成△XYZ,若△ABC的面积为1,求△XYZ的面积.
如图,△ABC中,D,E,F分别足BC,CA,AB边上的点,BD:DC=1:2,CE:EA=1:3,AF:FB=1:1,AD,BE,CF围成△XYZ,若△ABC的面积为1,求△XYZ的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com