
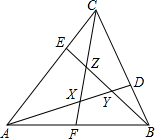
 如图,△ABC中,D,E,F分别足BC,CA,AB边上的点,BD:DC=1:2,CE:EA=1:3,AF:FB=1:1,AD,BE,CF围成△XYZ,若△ABC的面积为1,求△XYZ的面积.
如图,△ABC中,D,E,F分别足BC,CA,AB边上的点,BD:DC=1:2,CE:EA=1:3,AF:FB=1:1,AD,BE,CF围成△XYZ,若△ABC的面积为1,求△XYZ的面积. 分析 作出辅助线EG∥AB,得到相似三角形,用相似三角形的性质得到边的比,用同高的三角形的面积比等于对应边的比,如S△ACF=$\frac{1}{2}$S△ABC=$\frac{1}{2}$,再确定出S四边形AEZX=$\frac{7}{20}$即可,
解答 解:如图,过点E作EG∥AB,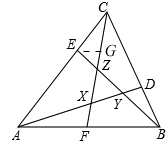
∵$\frac{AF}{FB}$=1
∴$\frac{AF}{AB}$=$\frac{1}{2}$,
∴S△ACF=$\frac{1}{2}$S△ABC=$\frac{1}{2}$,
∵$\frac{CE}{AE}$=$\frac{1}{3}$,
∴$\frac{CE}{AC}$=$\frac{1}{4}$,
∴S△BCE=$\frac{1}{4}$S△ABC=$\frac{1}{4}$,S△ABE=$\frac{3}{4}$,
∵EG∥AB,
∴$\frac{EG}{AF}$=$\frac{CE}{AC}$=$\frac{1}{4}$,
∵EG=AB,
∴$\frac{EZ}{ZB}$=$\frac{EG}{BF}$=$\frac{1}{4}$,
∴$\frac{EZ}{EB}$=$\frac{1}{5}$,
∴S△ZCE=$\frac{1}{5}$S△BCE=$\frac{1}{5}$×$\frac{1}{4}$=$\frac{1}{20}$,
同理:S△AFX=$\frac{1}{10}$,S△BDY=$\frac{1}{30}$,
∴S四边形AEZX=S△ACF-S△CEZ-S△AFX=$\frac{1}{2}$-$\frac{1}{20}$-$\frac{1}{10}$=$\frac{7}{20}$,
同理:S四边形FXYB=$\frac{1}{5}$,
∴S△XYZ=S△ABE-S四边形AEZX-S△AFX-S四边形FXYB=$\frac{3}{4}$-$\frac{7}{20}$-$\frac{1}{10}$-$\frac{1}{5}$=$\frac{1}{10}$.
点评 本题是面积等积变换的比较难的试题,主要考查同高的几个三角形的面积的比底的比,S△BCE=$\frac{1}{4}$S△ABC=$\frac{1}{4}$,S△ABE=$\frac{3}{4}$,涉及到的知识点有相似三角形的判定和性质,比的基本性质,解本题的关键是作出辅助线.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 300条 | B. | 380条 | C. | 400条 | D. | 420条 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
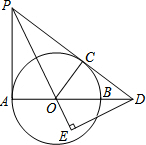 已知,如图,AB为⊙O的直径,PD切⊙O于点C,与AB的延长线交于点D,DE⊥PO交PO延长线于点E,连接PA,且∠EDB=∠EPA.
已知,如图,AB为⊙O的直径,PD切⊙O于点C,与AB的延长线交于点D,DE⊥PO交PO延长线于点E,连接PA,且∠EDB=∠EPA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
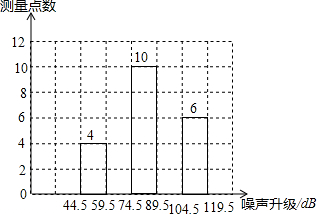 为了增强人们的环境保护意识,某校若干名学生组成了“控制噪声污染”课题学习研究小组.在环保局工作人员帮助指导下,该小组抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将调查的数据进行处理(设所测数据是正整数),得频数分布表如下:
为了增强人们的环境保护意识,某校若干名学生组成了“控制噪声污染”课题学习研究小组.在环保局工作人员帮助指导下,该小组抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将调查的数据进行处理(设所测数据是正整数),得频数分布表如下:| 组 别 | 噪声声级分组 | 频 数 | 频 率 |
| 1 | 44.5--59.5 | 4 | 0.1 |
| 2 | 59.5--74.5 | a | 0.2 |
| 3 | 74.5--89.5 | 10 | 0.25 |
| 4 | 89.5--104.5 | b | c |
| 5 | 104.5-119.5 | 6 | 0.15 |
| 合 计 | 40 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$-2 | B. | 2$\sqrt{5}$+2 | C. | 6-2$\sqrt{5}$ | D. | 6+2$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
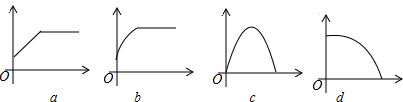
| A. | abcd | B. | dabc | C. | dbca | D. | cabd |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
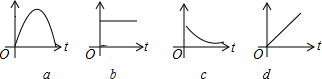
| A. | cdab | B. | acbd | C. | dabc | D. | cbad |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com