
| A. | 2$\sqrt{5}$-2 | B. | 2$\sqrt{5}$+2 | C. | 6-2$\sqrt{5}$ | D. | 6+2$\sqrt{5}$ |
分析 根据黄金分割的定义,知AC为较长线段,则AC=($\frac{\sqrt{5}-1}{2}$)AB,代入数据即可得出AB的值.
解答 解:∵C是线段AB的黄金分割点,且AC>BC,AC为较长线段,
∴AC=($\frac{\sqrt{5}-1}{2}$)AB,
∵AC=4,
∴4=($\frac{\sqrt{5}-1}{2}$)AB,
∴AB=2$\sqrt{5}$+2.
故选:B.
点评 本题考查了黄金分割,用到的知识点是把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值($\frac{\sqrt{5}-1}{2}$)叫做黄金比.


科目:初中数学 来源: 题型:解答题
 用圆规、直尺作图,不写作法,但要保留作图痕迹.
用圆规、直尺作图,不写作法,但要保留作图痕迹.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
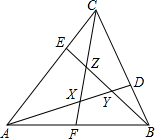 如图,△ABC中,D,E,F分别足BC,CA,AB边上的点,BD:DC=1:2,CE:EA=1:3,AF:FB=1:1,AD,BE,CF围成△XYZ,若△ABC的面积为1,求△XYZ的面积.
如图,△ABC中,D,E,F分别足BC,CA,AB边上的点,BD:DC=1:2,CE:EA=1:3,AF:FB=1:1,AD,BE,CF围成△XYZ,若△ABC的面积为1,求△XYZ的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
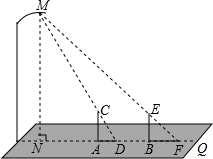 晚饭后,小林和小京在社区广场散步,两人在灯下沿直线NQ移动,如图,当小林正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小京正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小林的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小京身高BE的长.(结果精确到0.01米)
晚饭后,小林和小京在社区广场散步,两人在灯下沿直线NQ移动,如图,当小林正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小京正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小林的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小京身高BE的长.(结果精确到0.01米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com