
| A. | 12cm2 | B. | 96cm2 | C. | 48cm2 | D. | 24cm2 |
分析 先求出菱形的边长,然后设菱形的两对角线分别为8x,6x,根据菱形的对角线垂直平分求出两对角线的一半,再利用勾股定理列式求出x,从而得到对角线的长,然后根据菱形的面积等于对角线乘积的一半列式进行计算即可得解.
解答 解:∵菱形的周长是20cm,
∴边长为20÷4=5cm,
∵两条对角线的比是4:3,
∴设菱形的两对角线分别为8x,6x,
根据菱形的性质可知,菱形的对角线互相垂直平分,
则对角线的一半分别为4x,3x,
根据勾股定理得,(4x)2+(3x)2=52,
解得x=1,
所以,两对角线分别为8cm,6cm,
所以,这个菱形的面积=$\frac{1}{2}$×8×6=24cm2.
故选:D.
点评 本题考查了菱形的性质,勾股定理的应用,主要利用了菱形的对角线互相垂直平分的性质,以及菱形的面积等于对角线乘积的一半.


科目:初中数学 来源: 题型:解答题
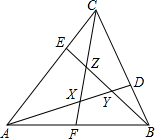 如图,△ABC中,D,E,F分别足BC,CA,AB边上的点,BD:DC=1:2,CE:EA=1:3,AF:FB=1:1,AD,BE,CF围成△XYZ,若△ABC的面积为1,求△XYZ的面积.
如图,△ABC中,D,E,F分别足BC,CA,AB边上的点,BD:DC=1:2,CE:EA=1:3,AF:FB=1:1,AD,BE,CF围成△XYZ,若△ABC的面积为1,求△XYZ的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | -1 | D. | 2015 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
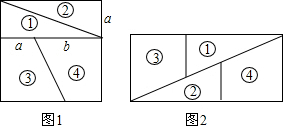
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一条笔直的路上A,B,C村庄的位置如图所示,甲从B村出发,向C村方向匀速行驶,经过30分钟,距A村15千米,经过2个小时,距A村30千米,此时乙从B村出发,也向C村方向匀速行驶.
一条笔直的路上A,B,C村庄的位置如图所示,甲从B村出发,向C村方向匀速行驶,经过30分钟,距A村15千米,经过2个小时,距A村30千米,此时乙从B村出发,也向C村方向匀速行驶.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com