
| A. | 2 | B. | $\frac{1}{2}$ | C. | -1 | D. | 2015 |
分析 根据这组数的运算规则找出该数列的前几项,能够发现a4=a1,从而得出该组数量每3项一循环的规律,结合2015÷3余2可得出结论.
解答 解:当a1=2时,a2=1-$\frac{1}{{a}_{1}}$=$\frac{1}{2}$,a3=1-$\frac{1}{{a}_{2}}$=-1,a4=1-$\frac{1}{{a}_{3}}$=2=a1,
由此发现,该数列每3个一循环,
∵2015÷3=671…2,
∴a2015=a2=$\frac{1}{2}$.
故选B.
点评 本题考查了数字的变化,解题的关键是列出数列的前几项找出“每3项一循环”的规律.本题属于中档题,难度不大,解决该题型题目时,找出数列前几项发现规律是关键.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
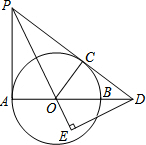 已知,如图,AB为⊙O的直径,PD切⊙O于点C,与AB的延长线交于点D,DE⊥PO交PO延长线于点E,连接PA,且∠EDB=∠EPA.
已知,如图,AB为⊙O的直径,PD切⊙O于点C,与AB的延长线交于点D,DE⊥PO交PO延长线于点E,连接PA,且∠EDB=∠EPA.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
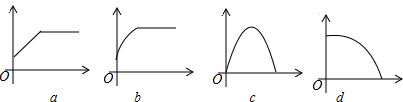
| A. | abcd | B. | dabc | C. | dbca | D. | cabd |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
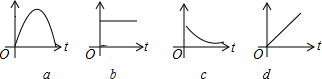
| A. | cdab | B. | acbd | C. | dabc | D. | cbad |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com