
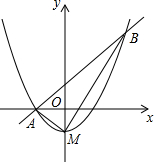
 如图,顶点M(0,-1)在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,连结AM,BM.
如图,顶点M(0,-1)在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,连结AM,BM.分析 (1)由点A是直线y=x+1与x轴的交点可求出点A的坐标,将抛物线的解析式设成顶点式,然后把点A的坐标代入该解析式,就可解决问题;
(2)只需解直线与抛物线的解析式组成的方程组,然后解这个方程组就可解决问题;
(3)将平移后的抛物线的解析式设成顶点式,然后把y=x代入该解析式,得到关于x的一元二次方程,要使平移后的抛物线总有不动点,只需该一元二次方程的根的判别式大于等于0即可.
解答 解:∵点A是直线y=x+1与x轴的交点,
∴A(-1,0).
设顶点为(0,-1)的抛物线的解析式为y=ax2-1,
∵点A(-1,0)在抛物线y=ax2-1上,
∴0=a-1,
∴a=1,
∴抛物线的解析式为y=x2-1;
(2)解方程组$\left\{\begin{array}{l}{y=x+1}\\{y={x}^{2}-1}\end{array}\right.$,得$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=0}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=3}\end{array}\right.$,
故点B的坐标为(2,3);
(3)设平移后的抛物线的解析式为y=(x-m)2+2m,
把y=x代入y=(x-m)2+2m,得
x=(x-m)2+2m,
整理得,x2-(2m+1)x+m2+2m=0,
由题可得△=(2m+1)2-4×1×(m2+2m)=1-4m≥0,
解得m≤$\frac{1}{4}$.
故当m≤$\frac{1}{4}$时,平移后的抛物线总有不动点.
点评 本题主要考查了直线上点的坐标特征、运用待定系数法求抛物线的解析式、求直线与抛物线的解析式的交点、根的判别式等知识,通常可将直线与抛物线的交点问题转化为一元二次方程解的问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
| 购物总金额(原价) | 折扣率 |
| 不超过3000元的部分 | 九折 |
| 超过3000元但不超过5000元的部分 | 八折 |
| 超过5000元的部分 | 七折 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
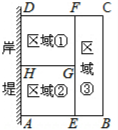 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块长方形区域,而且这三块长方形区域的面积相等.设BC的长度为xm,AB为ym.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块长方形区域,而且这三块长方形区域的面积相等.设BC的长度为xm,AB为ym.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com