
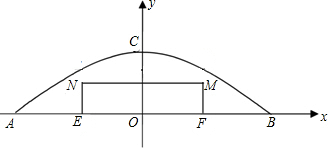
分析 (1)根据题意可设抛物线解析式为y=ax2+c,将点C(0,5),点B(10,0)代入求得a、c的值即可求解;
(2)令x=5求得y的值,将y的值减去0.35可得广告牌最大高度.
解答 解:(1)根据题意,设抛物线解析式为y=ax2+c,
将点C(0,5),点B(10,0)代入,得:
$\left\{\begin{array}{l}{100a+c=0}\\{c=5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{20}}\\{c=5}\end{array}\right.$.
故抛物线解析式为:y=-$\frac{1}{20}$x2+5;
(2)当x=5时,y=-$\frac{1}{20}$×25+5=3.75(m),
3.75-0.35=3.4(m).
答:矩形广告牌的最大高度为3.4m.
点评 本题主要考查二次函数的实际应用,根据题意设出函数解析式是根本,待定系数法求得抛物线解析式是解题关键.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:解答题
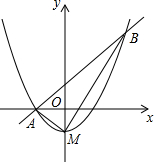 如图,顶点M(0,-1)在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,连结AM,BM.
如图,顶点M(0,-1)在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,连结AM,BM.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 步行人数为30人 | B. | 骑车人数占总人数的10% | ||
| C. | 该班总人数为50人 | D. | 乘车人数是骑车人数的40% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组:$\left\{\begin{array}{l}{3(x-2)≤x-4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$并将其解集表示在如图所示的数轴上.
解不等式组:$\left\{\begin{array}{l}{3(x-2)≤x-4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$并将其解集表示在如图所示的数轴上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
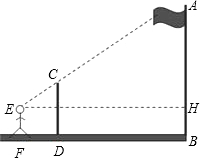 九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,如图所示,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,则旗杆AB的高度13.5m.
九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,如图所示,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,则旗杆AB的高度13.5m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com