
 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
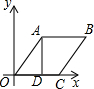 请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我军某部队上午9时在南海巡航,某军舰位于南海的A处,观察到一小岛P位于军舰的北偏西67.5°,军舰以21海里/时的速度向正北方向行驶,下午2时军舰到达B处,这时观测到城市P位于军舰的南偏西36.9°方向,求此时军舰所在B处与城市P的距离?(参考数据:sin36.9°≈$\frac{3}{5}$,tan36.9°≈$\frac{3}{4}$,sin67.5°≈$\frac{12}{13}$,tan67.5°≈$\frac{12}{5}$)
我军某部队上午9时在南海巡航,某军舰位于南海的A处,观察到一小岛P位于军舰的北偏西67.5°,军舰以21海里/时的速度向正北方向行驶,下午2时军舰到达B处,这时观测到城市P位于军舰的南偏西36.9°方向,求此时军舰所在B处与城市P的距离?(参考数据:sin36.9°≈$\frac{3}{5}$,tan36.9°≈$\frac{3}{4}$,sin67.5°≈$\frac{12}{13}$,tan67.5°≈$\frac{12}{5}$)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
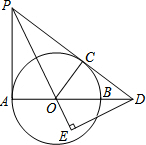 已知,如图,AB为⊙O的直径,PD切⊙O于点C,与AB的延长线交于点D,DE⊥PO交PO延长线于点E,连接PA,且∠EDB=∠EPA.
已知,如图,AB为⊙O的直径,PD切⊙O于点C,与AB的延长线交于点D,DE⊥PO交PO延长线于点E,连接PA,且∠EDB=∠EPA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
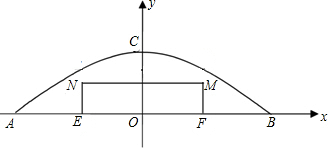
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
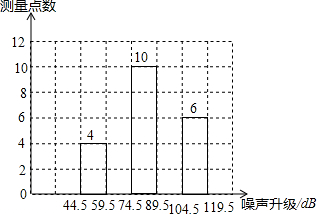 为了增强人们的环境保护意识,某校若干名学生组成了“控制噪声污染”课题学习研究小组.在环保局工作人员帮助指导下,该小组抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将调查的数据进行处理(设所测数据是正整数),得频数分布表如下:
为了增强人们的环境保护意识,某校若干名学生组成了“控制噪声污染”课题学习研究小组.在环保局工作人员帮助指导下,该小组抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将调查的数据进行处理(设所测数据是正整数),得频数分布表如下:| 组 别 | 噪声声级分组 | 频 数 | 频 率 |
| 1 | 44.5--59.5 | 4 | 0.1 |
| 2 | 59.5--74.5 | a | 0.2 |
| 3 | 74.5--89.5 | 10 | 0.25 |
| 4 | 89.5--104.5 | b | c |
| 5 | 104.5-119.5 | 6 | 0.15 |
| 合 计 | 40 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com