
分析 (1)仿照例题,代入数据求值;对应1+2+3+…+n来说,我们发现第一项和最后一项,第二项和倒数第二项…它们的和相等,即能得出1+2+3+…+n=$\frac{n(n+1)}{2}$,将其代入例题给定算式中即可得出结论;
(2)结合给定例题与(1)中的结论,代入数据即可求出结果;
(3)将原式补全,加上13+23+33+…+103再减去13+23+33+…+103,将数据代入(1)的结论中即可算出结果.
解答 解:(1)根据给定例子可知:
13+23+33+43+53=(1+2+3+4+5)2=225;
13+23+33+…+n3=(1+2+3+…+n)2=$[\frac{n(n+1)}{2}]^{2}$.
故答案为:1+2+3+4+5+6;225;1+2+3+…+n;$\frac{n(n+1)}{2}$.
(2)13+23+…+493+503=(1+2+3+…+50)2=$(\frac{50×51}{2})^{2}$=12752=1625625.
(3)113+123+…+983+993的=(1+2+3…+99)2-(1+2+3+…+10)2=$(\frac{99×100}{2})^{2}$-$(\frac{10×11}{2})^{2}$=49502-552=24499475.
点评 本题考查了数字的变化,解题的关键是根据给定例题以及数列求和找出13+23+33+…+n3=$[\frac{n(n+1)}{2}]^{2}$.本题属于中档题,难度不大,但在数列求和处需做特殊说明,毕竟初中没有学到等差数列的求和公式.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
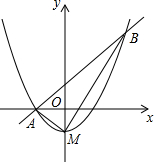 如图,顶点M(0,-1)在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,连结AM,BM.
如图,顶点M(0,-1)在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,连结AM,BM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
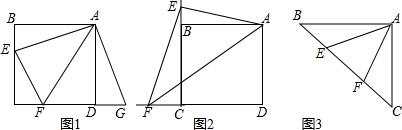
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 △ABC在直角坐标系中的位置如图所示,若将△ABC绕点O旋转,点C的对应点为点D,其中A(1,2),B(-1,0),C(3,-1),D(-1,-3),则旋转后点A的对应点E的坐标为( )
△ABC在直角坐标系中的位置如图所示,若将△ABC绕点O旋转,点C的对应点为点D,其中A(1,2),B(-1,0),C(3,-1),D(-1,-3),则旋转后点A的对应点E的坐标为( )| A. | (-1,2) | B. | (0,-1) | C. | (1,-3) | D. | (2,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 步行人数为30人 | B. | 骑车人数占总人数的10% | ||
| C. | 该班总人数为50人 | D. | 乘车人数是骑车人数的40% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com