
分析 (1)根据零指数幂、负整数指数幂、特殊角的三角函数值可以解答本题;
(2)先对原式化简,再将a=1,b=-2代入化简后的式子即可解答本题.
解答 (1)解:原式=1+2-(-2)+2×$\frac{\sqrt{2}}{2}$
=1+2+2+$\sqrt{2}$
=5+$\sqrt{2}$;
(2)解:原式=$1-\frac{a-b}{a+2b}•\frac{{{{({a+2b})}^2}}}{{({a+b})({a-b})}}$
=$1-\frac{{a+2{b^{\;}}}}{a+b}$
=$\frac{a+b-a-2b}{a+b}$
=$-\frac{b}{a+b}$
当a=1,b=-2时,
原式=$-\frac{-2}{1-2}=-2$.
点评 本题考查分式的化简求值、负整数指数幂、实数的运算、零指数幂、特殊角的三角函数值,解题的关键是明确它们各自的含义,可以对原式化简求值.


科目:初中数学 来源: 题型:选择题
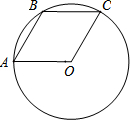 已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )
已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )| A. | ∠AOC=120° | |
| B. | 四边形OABC一定是菱形 | |
| C. | 若连接AC,则AC=$\sqrt{2}$OA | |
| D. | 若连接AC、BO,则AC与BO互相垂直平分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
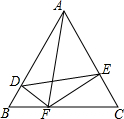 如图,△ABC是边长为a的等边三角形,DF⊥AB,EF⊥AC.
如图,△ABC是边长为a的等边三角形,DF⊥AB,EF⊥AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
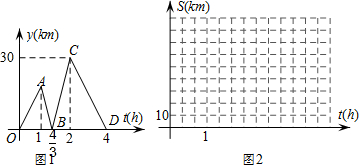
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
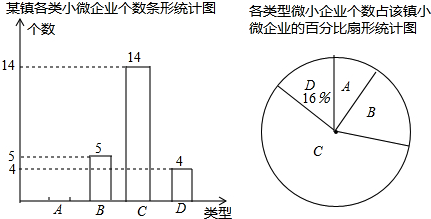
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com