
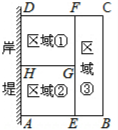
 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块长方形区域,而且这三块长方形区域的面积相等.设BC的长度为xm,AB为ym.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块长方形区域,而且这三块长方形区域的面积相等.设BC的长度为xm,AB为ym.分析 (1)根据三个矩形面积相等,得到矩形AEFD面积是矩形BCFE面积的2倍,可得出AE=2BE,设BE=a,则有AE=2a,表示出a与3a,进而表示出y与x的关系式,并求出x的范围即可;
(2)根据:长×宽=长方形面积,列出方程求解可得.
解答 解:(1)∵三块矩形区域的面积相等,
∴矩形AEFD面积是矩形BCFE面积的2倍,
∴AE=2BE,
设BE=a,则AE=2a,
∴8a+2x=80,
∴a=-$\frac{1}{4}$x+10,3a=-$\frac{3}{4}$x+30,
∴$y=30-\frac{3}{4}x$.
∴y与x之间的函数关系式$y=30-\frac{3}{4}x$(0<x<40).
(2)根据题意,得:$x({30-\frac{3}{4}x})=300$,
解得:x1=x2=20,
∴当BC=20m时,长方形面积为300m2.
点评 本题主要考查二次函数的实际应用能力,根据三块矩形区域的面积相等边长间的关系是解题的突破点,也是列函数解析式的关键.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | + | B. | - | C. | × | D. | ÷ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
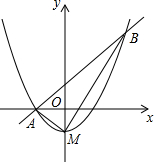 如图,顶点M(0,-1)在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,连结AM,BM.
如图,顶点M(0,-1)在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,连结AM,BM.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com