练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．已知x=$\sqrt{3}$-2，求代数式（5+2$\sqrt{3}$）x2+（2+$\sqrt{3}$）x+$\sqrt{3}$的值．

    分析 直接将x的值代入再利用完全平方公式以及平方差公式计算得出答案．

    解答 解：∵x=$\sqrt{3}$-2，
    ∴（5+2$\sqrt{3}$）x2+（2+$\sqrt{3}$）x+$\sqrt{3}$
    =（5+2$\sqrt{3}$）（$\sqrt{3}$-2）2+（2+$\sqrt{3}$）（$\sqrt{3}$-2）+$\sqrt{3}$
    =（5+2$\sqrt{3}$）（5-2$\sqrt{3}$）+（3-4）+$\sqrt{3}$
    =25-12-1+$\sqrt{3}$
    =12+$\sqrt{3}$．

    点评 此题主要考查了二次根式的混合运算，熟练应用乘法公式是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    16．在平行四边形ABCD中，P为对角线BD上任意一点，连接PA、PC，得到△PAB、△PBC、△PCD、△PDA，设它们的面积分别是S1、S2、S3、S4，给出如下结论：①S1=S2；②S1+S2=S3；③S1+S3=S2+S4；④若S1•S3=S2•S4，其中正确结论的序号是③．（在横线上填上你认为所有正确答案的序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．如图，在下列四组条件中，能判定AB∥CD的是（　　）
    A．∠1=∠3B．∠2=∠4C．∠CAB=∠ACDD．∠CAB+∠ACD=180°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算：
    （1）$\root{3}{\frac{27}{64}}$+$\sqrt{\frac{1}{16}}$                     
    （2）|$\sqrt{2}$-$\sqrt{3}$|+2$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．（$\sqrt{2}$-$\sqrt{3}$）2015•（$\sqrt{2}$+$\sqrt{3}$）2016=-$\sqrt{2}$-$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．已知m=$\sqrt{9-x}$，n=$\sqrt{72}$，p=$\sqrt{15}$．
    （1）当x=-1时，求（p+m）（p-m）+n的值；
    （2）若m，n，p为Rt△ABC的三边长，求x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．用加减法解下列方程组：
    （1）$\left\{\begin{array}{l}{2x+5y=5}\\{3x-5y=10}\end{array}\right.$
    （2）$\left\{\begin{array}{l}{3x+2y=5}\\{2x+5y=7}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．三位老师周末到某家电专卖店购买冰箱和空调，正值该专卖店举行“迎新春、大优惠”活动，具体优惠情况如下表：
      购物总金额（原价）折扣率
    不超过3000元的部分九折
    超过3000元但不超过5000元的部分八折
    超过5000元的部分七折
    （1）李老师所购物品的原价是6000元，李老师实际付5000元
    （2）已知张老师购买了两件物品（一个冰箱和一个空调）共付费4060元．请问这两件物品的原价总共是多少元？
    （3）碰巧同一天赵老师也在同一家专卖店购买了同样的两件物品．但赵老师上午去购买的冰箱，下 午去购买的空调，如此一来赵老师两次付款总额比张老师多花费了140元．已知此冰箱的原价比空调的原价要贵，求这两件物品的原价分别为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

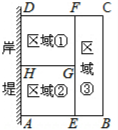    7．为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为80m的围网在水库中围成了如图所示的①②③三块长方形区域，而且这三块长方形区域的面积相等．设BC的长度为xm，AB为ym．
    （1）求y与x之间的函数关系式，并注明自变量x的取值范围；
    （2）当BC为多长时，长方形面积达300m2？

    查看答案和解析>>

    同步练习册答案