
 …ηkΓΌ0Θ§»τΚ· ΐy1=Θ®x-kΘ©2+2kΚΆy2=-Θ®x+kΘ©2-2kΒΡΆΦœσ”κy÷α“ά¥ΈΫΜ”ΎAΘ§BΝΫΒψΘ§Κ· ΐy1Θ§y2ΒΡΆΦœσΒΡΕΞΒψΖ÷±πΈΣCΘ§DΘ°
…ηkΓΌ0Θ§»τΚ· ΐy1=Θ®x-kΘ©2+2kΚΆy2=-Θ®x+kΘ©2-2kΒΡΆΦœσ”κy÷α“ά¥ΈΫΜ”ΎAΘ§BΝΫΒψΘ§Κ· ΐy1Θ§y2ΒΡΆΦœσΒΡΕΞΒψΖ÷±πΈΣCΘ§DΘ°Ζ÷Έω Θ®1Θ©»Γk=1Ω…ΒΟΝΫΚ· ΐΫβΈω ΫΘ§≤ΔΉς≥ω≤ίΆΦΘΜ
Θ®2Θ©”…Κ· ΐΫβΈω Ϋ«σ≥ωAΘ§BΘ§CΘ§DΒΡΉχ±ξΘ§Ϋχ“Μ≤Ϋ«σΒΟABΘ§άϊ”ΟΕΰ¥ΈΚ· ΐ–‘÷ «σΒΟΖΕΈßΘΜ
Θ®3Θ©ΗυΨίAΘ§BΘ§CΘ§DΥΡΒψΉχ±ξΘ§άϊ”ΟΕ‘≥ΤΒΡ–‘÷ Θ§Ω…“‘÷ΛΟςΙΙΥΡ±Ώ–ΈADBC «ΤΫ––ΥΡ±Ώ–ΈΘ§‘ΌΗυΨίOA=OC ±ΥΡ±Ώ–Έ «ΨΊ–ΈΘ§Ν–≥ωΖΫ≥ΧΫβΨωΘ§”…”ΎΒψCΓΔD≤Μ‘Ύx÷α…œΘ§Υυ“‘≤ΜΩ…Ρή «Νβ–ΈΘ°
Ϋβ¥π ΫβΘΚΘ®1Θ©k=1 ±Θ§y1=Θ®x-1Θ©2+2ΚΆy2=-Θ®x+1Θ©2-2ΒΡΆΦœσ»γΆΦΥυ ΨΘ§’βΝΫΗωΚ· ΐΆΦœσΙΊ”Ύ‘≠ΒψΕ‘≥ΤΘ°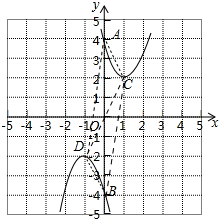
Θ®2Θ©ΓΏΒψAΘ®0Θ§k2+2kΘ§Θ©Θ§BΘ®0Θ§-k2-2kΘ©Θ§
ΓύAB=|k2+2k-Θ®-k2-2kΘ©|=|2k2+4k|Θ§
ΓΏ-2ΘΦkΘΦ0Θ§
ΓύAB «Ήν–Γ÷ΒΈΣOΘ§Ήν¥σ÷ΒΈΣ2Θ§
Γύ0ΘΦABΓή2Θ°
Θ®3Θ©ΓΏΒψAΘ®0Θ§k2+2kΘ§Θ©Θ§BΘ®0Θ§-k2-2kΘ©Θ§CΘ®kΘ§2kΘ©Θ§DΘ®-kΘ§-2kΘ©Θ§
ΓύAΓΔBΙΊ”Ύ‘≠ΒψΕ‘≥ΤΘ§CΓΔDΙΊ”Ύ‘≠ΒψΕ‘≥ΤΘ§
ΓύOA=OBΘ§OC=ODΘ§
ΓύΥΡ±Ώ–ΈADBC «ΤΫ––ΥΡ±Ώ–ΈΘ°
Β±OA=OC ±Θ§ΥΡ±Ώ–ΈADBC «ΨΊ–ΈΘ§¥Υ ±k2+2k=Γά$\sqrt{5}$kΘ§k=$\sqrt{5}$-2Μρ-$\sqrt{5}$-2Θ§
Β±OAΓΆOC ±Θ§ΥΡ±Ώ–ΈADBC «Νβ–ΈΘ§¥Υ ±ΒψCΓΔD‘Ύx÷α…œΘ§”κkΓΌ0Ο§ΕήΘ°
ΓύΥΡ±Ώ–ΈADBC≤ΜΩ…Ρή «Νβ–ΈΘ°
ΒψΤά ±ΨΧβΩΦ≤ιΕΰ¥ΈΚ· ΐΒΡΆΦœσΓΔΤΫ––ΥΡ±Ώ–ΈΒΡ≈–Ε®ΓΔΨΊ–ΈΒΡ≈–Ε®ΓΔΝβ–ΈΒΡ≈–Ε®ΓΔΕ‘≥ΤΒ»÷Σ ΕΘ§ΫβΧβΒΡΙΊΦϋ «άϊ”ΟΕ‘≥ΤΒΡ–‘÷ Θ§ τ”Ύ÷–ΩΦ≥ΘΩΦΧβ–ΆΘ§Χεœ÷ΝΥ ΐ–ΈΫαΚœΒΡΫβΧβΥΦœκΖΫΖ®Θ§ «÷–ΒΒΧβΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $\left\{\begin{array}{l}x=2\\ y=-4\end{array}\right.$ | BΘ° | $\left\{\begin{array}{l}x=2\\ y=4\end{array}\right.$ | CΘ° | $\left\{\begin{array}{l}x=-2\\ y=4\end{array}\right.$ | DΘ° | $\left\{\begin{array}{l}x=-2\\ y=-4\end{array}\right.$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 6Ήι | BΘ° | 7Ήι | CΘ° | 8Ήι | DΘ° | 9Ήι |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | -3 | BΘ° | 0 | CΘ° | -2 | DΘ° | 1 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
 »γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§Εΰ¥ΈΚ· ΐy=$\frac{1}{3}{x^2}$+bx+cΒΡΆΦœσ”κy÷αΫΜ”ΎΒψAΘ§”κΥΪ«ζœΏy=$\frac{8}{x}$”–“ΜΗωΙΪΙ≤ΒψBΘ§ΥϋΒΡΚαΉχ±ξΈΣ4Θ§ΙΐΒψBΉς÷±œΏlΓΈx÷αΘ§”κΗΟΕΰ¥ΈΚ· ΐΆΦœσΫΜ”ΎΝμ“ΜΗωΒψCΘ§÷±œΏAC‘Ύy÷α…œΒΡΫΊΨύ «-6Θ°
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§Εΰ¥ΈΚ· ΐy=$\frac{1}{3}{x^2}$+bx+cΒΡΆΦœσ”κy÷αΫΜ”ΎΒψAΘ§”κΥΪ«ζœΏy=$\frac{8}{x}$”–“ΜΗωΙΪΙ≤ΒψBΘ§ΥϋΒΡΚαΉχ±ξΈΣ4Θ§ΙΐΒψBΉς÷±œΏlΓΈx÷αΘ§”κΗΟΕΰ¥ΈΚ· ΐΆΦœσΫΜ”ΎΝμ“ΜΗωΒψCΘ§÷±œΏAC‘Ύy÷α…œΒΡΫΊΨύ «-6Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 1Ηω | BΘ° | 2Ηω | CΘ° | 3Ηω | DΘ° | 4Ηω |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 300Χθ | BΘ° | 380Χθ | CΘ° | 400Χθ | DΘ° | 420Χθ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
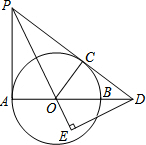 “―÷ΣΘ§»γΆΦΘ§ABΈΣΓ―OΒΡ÷±ΨΕΘ§PD«–Γ―O”ΎΒψCΘ§”κABΒΡ―”≥ΛœΏΫΜ”ΎΒψDΘ§DEΓΆPOΫΜPO―”≥ΛœΏ”ΎΒψEΘ§Ν§Ϋ”PAΘ§«“ΓœEDB=ΓœEPAΘ°
“―÷ΣΘ§»γΆΦΘ§ABΈΣΓ―OΒΡ÷±ΨΕΘ§PD«–Γ―O”ΎΒψCΘ§”κABΒΡ―”≥ΛœΏΫΜ”ΎΒψDΘ§DEΓΆPOΫΜPO―”≥ΛœΏ”ΎΒψEΘ§Ν§Ϋ”PAΘ§«“ΓœEDB=ΓœEPAΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com