
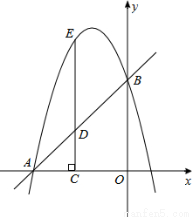
如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,过A、B两点的抛物线为y=-x2+bx+c.点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.
(1)求抛物线的解析式.
(2)当DE=4时,求四边形CAEB的面积.
(3)连接BE,是否存在点D,使得△DBE和△DAC相似?若存在,直接写出点D坐标;若不存在,说明理由.
(1) y=-x2-3x+4.(2)12.(3) (-3,1)或(-2,2).
【解析】
试题分析:(1)首先求出点A、B的坐标,然后利用待定系数法求出抛物线的解析式;
(2)设点C坐标为(m,0)(m<0),根据已知条件求出点E坐标为(m,8+m);由于点E在抛物线上,则可以列出方程求出m的值.在计算四边形CAEB面积时,利用S四边形CAEB=S△ACE+S梯形OCEB-S△BCO,可以简化计算;
(3)由于△ACD为等腰直角三角形,而△DBE和△DAC相似,则△DBE必为等腰直角三角形.分两种情况讨论,要点是求出点E的坐标,由于点E在抛物线上,则可以由此列出方程求出未知数.
试题解析:(1)在直线解析式y=x+4中,令x=0,得y=4;令y=0,得x=-4,
∴A(-4,0),B(0,4).
∵点A(-4,0),B(0,4)在抛物线y=-x2+bx+c上,
∴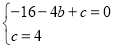 ,
,
解得:b=-3,c=4,
∴抛物线的解析式为:y=-x2-3x+4.
(2)设点C坐标为(m,0)(m<0),则OC=-m,AC=4+m.
∵OA=OB=4,
∴∠BAC=45°,
∴△ACD为等腰直角三角形,
∴CD=AC=4+m,
∴CE=CD+DE=4+m+4=8+m,
∴点E坐标为(m,8+m).
∵点E在抛物线y=-x2-3x+4上,
∴8+m=-m2-3m+4,解得m1=m2=-2.
∴C(-2,0),AC=OC=2,CE=6,
S四边形CAEB=S△ACE+S梯形OCEB-S△BCO
=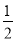 ×2×6+
×2×6+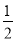 (6+4)×2-
(6+4)×2-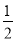 ×2×4=12.
×2×4=12.
(3)设点C坐标为(m,0)(m<0),则OC=-m,CD=AC=4+m,BD=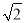 OC=-
OC=-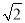 m,则D(m,4+m).
m,则D(m,4+m).
∵△ACD为等腰直角三角形,△DBE和△DAC相似
∴△DBE必为等腰直角三角形.
i)若∠BED=90°,则BE=DE,
∵BE=OC=-m,
∴DE=BE=-m,
∴CE=4+m-m=4,
∴E(m,4).
∵点E在抛物线y=-x2-3x+4上,
∴4=-m2-3m+4,解得m=0(不合题意,舍去)或m=-3,
∴D(-3,1);
ii)若∠EBD=90°,则BE=BD=-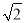 m,
m,
在等腰直角三角形EBD中,DE=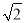 BD=-2m,
BD=-2m,
∴CE=4+m-2m=4-m,
∴E(m,4-m).
∵点E在抛物线y=-x2-3x+4上,
∴4-m=-m2-3m+4,解得m=0(不合题意,舍去)或m=-2,
∴D(-2,2).
综上所述,存在点D,使得△DBE和△DAC相似,点D的坐标为(-3,1)或(-2,2).
考点:二次函数综合题.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源:2014-2015学年河南省九年级下学期第一次月考数学试卷(解析版) 题型:选择题
如果一元二次方程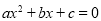 (
(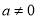 )满足
)满足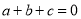 那么我们称这个方程为“凤凰”方程.已知
那么我们称这个方程为“凤凰”方程.已知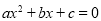 (
(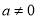 )是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是( )
)是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是( )
A.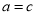 B.
B.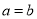 C.
C.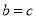 D.
D.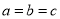
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省漯河市九年级上期末模拟数学试卷(解析版) 题型:解答题
如图,在△ABC中,AC⊥BC,D是BC延长线上的一点,E是AC上的一点,连接ED,∠A=∠D.

(1)求证:△ABC∽△DEC;
(2)若AC=3,AE=1,BC=4,求DE的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省漯河市九年级上期末模拟数学试卷(解析版) 题型:选择题
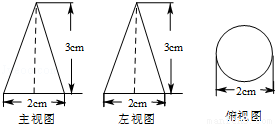
如图是一个几何体的三视图,则这个几何体的侧面积是__________ cm2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省腾冲县七年级上学期六校联考期末数学试卷(解析版) 题型:解答题
解方程:(每小题4分,共8分)
(1)5x+2(3x-7)=9-4(2+x)
(2) 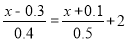
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com