
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017届甘肃兰州市九年级中考模拟数学试卷(解析版) 题型:解答题
如图,在直角体系中,直线AB交x轴于点A(5,0),交y轴于点B,AO是⊙M的直径,其半圆交AB于点C,且AC=3。取BO的中点D,连接CD、MD和OC。
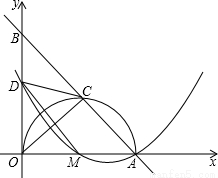
(1)求证:CD是⊙M的切线;
(2)二次函数的图象经过点D、M、A,其对称轴上有一动点P,连接PD、PM,求△PDM的周长最小时点P的坐标;
(3)在(2)的条件下,当△PDM的周长最小时,抛物线上是否存在点Q,使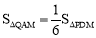 ?若存在,求出点Q的坐标;若不存在,请说明理由。
?若存在,求出点Q的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源:2017届广东省汕头市澄海区九年级5月中考模拟数学试卷(解析版) 题型:解答题
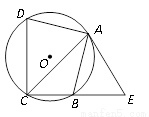
如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.
(1)求证:AE是⊙O的切线;
(2)若AB=AD,AC= ,tan∠ADC=3,求BE的长.
,tan∠ADC=3,求BE的长.
查看答案和解析>>
科目:初中数学 来源:2017届广东省汕头市澄海区九年级5月中考模拟数学试卷(解析版) 题型:单选题
如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠2=80°,那么∠3的度数为( )
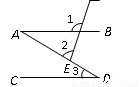
A. 40° B. 50° C. 60° D. 70°
查看答案和解析>>
科目:初中数学 来源:2017届福建省九年级下学期第二次质量检测数学试卷(解析版) 题型:解答题
若抛物线L:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.
(1)若直线y=mx+1与抛物线y=x2﹣2x+n具有“一带一路”关系,求m,n的值;
(2)若某“路线”L的顶点在反比例函数y=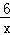 的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
(3)当常数k满足 ≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
查看答案和解析>>
科目:初中数学 来源:2017届福建省九年级下学期第二次质量检测数学试卷(解析版) 题型:单选题
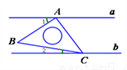
如图,等腰直角三角板的顶点A,C分别在直线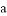 ,
,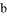 上.若
上.若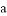 ∥
∥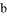 ,
,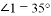 ,则
,则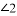 的度数为( )
的度数为( )
A. 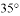 B.
B. 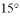 C.
C. 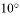 D.
D. 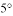
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com