
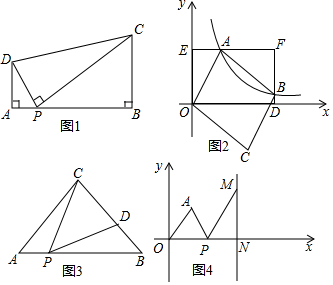
���� ��1�����ͼ1�����ò����е�֪ʶ�õ���OE•BF=AE•AF�����ݵ��������ͼ�ε����ʣ�����������ͼ���ϵ����������������õ�B�����ꣻ
��2�����ͼ2�����ݲ����е�֪ʶ�õ���ʽ��AC•BD=AP•BP�������֪�����õ�����߶εij��ȣ�������ֵ���ɣ�
��3����x����ȡ��C��ʹ�á�NCM=��APM=��AOP�����P������Ϊ��x��0�����ɣ�1���ã�AO•MC=OP•PC��������߶εij��ȴ��������õ���x2-��7+3y��x+25y=0���ɸ����б�ʽ��֪[-��7+3y��]2-4��25y=9y2-58y+49=��9y-49����y-1����0���ɴ������ֵ��
��� 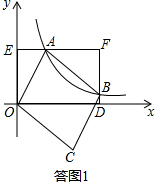 �⣺��1�����ͼ1����A��2��4���ڷ���������y=$\frac{k}{x}$��x��0����ͼ���ϣ�
�⣺��1�����ͼ1����A��2��4���ڷ���������y=$\frac{k}{x}$��x��0����ͼ���ϣ�
��k=xy=2��4=8��
��������ʽ�ǣ�y=$\frac{8}{x}$��
��B��a��$\frac{8}{a}$����
������ã�OE=4��BF=4-$\frac{8}{a}$��AE=2��AF=a-2��
����OE•BF=AE•AF�õ���4��4-$\frac{8}{a}$��=2��a-2����
���a=8��
�ʵ�B������Ϊ����8��1����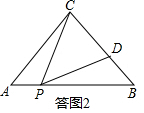
�ʴ��ǣ���8��1����
��2�����ͼ2�������⣬�ã�AP=t��BP=6-t��
��AC=BC����A=��B=��CPD��
��AC•BD=AP•BP��
��4s=t��6-t��=6t-t2��
��s=$-\frac{1}{4}{��t-3��^2}+\frac{9}{4}$��
��t=3ʱ��t�����ֵΪ$\frac{9}{4}$����ʱCD����СֵΪ4-$\frac{9}{4}$=$\frac{17}{4}$��
��3����x����ȡ��C��ʹ�á�NCM=��APM=��AOP�����P������Ϊ��x��0����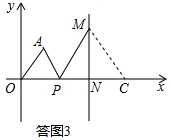 ����AO=$\sqrt{{3^2}+{4^2}}$=5��
����AO=$\sqrt{{3^2}+{4^2}}$=5��
�ɣ�1���ã�AO•MC=OP•PC������tan��NCM=tan��APM=$\frac{4}{3}$��
��Rt��MNC�У���CN=3y����MN=4y���ɹ��ɶ�������MC=$\sqrt{{{��3y��}^2}+{{��4y��}^2}}$=5y��
��OP=x��PC=7+3y-x��
��5��5y=x��7+3y-x����
�������ã�x2-��7+3y��x+25y=0��
��x��ֵ�Ǵ��ڵģ�
��̸����б�ʽ=[-��7+3y��]2-4��25y=9y2-58y+49=��9y-49����y-1����0��
��y��1��y��$\frac{49}{9}$����ȥ����4y=4��
��ˣ�MN�����ֵΪ4��
���� ���⿼���˷����������ۺ��⣬�������մ���ϵ����ȷ��������ϵʽ�����ɶ��������κ�����ֵ�������������ͼ�ε����ʵ�֪ʶ�㣬���Ⲣ����ͼ1���ṩ�ĵ�ʽ�ǽ���Ĺؼ���


 ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����Rt��ABC�У���C=90�㣬��BAC=60�㣬AMΪ��BAC��ƽ���ߣ���BC=20cm����AM�ij�Ϊ$\frac{40}{3}$cm��
��ͼ��ʾ����Rt��ABC�У���C=90�㣬��BAC=60�㣬AMΪ��BAC��ƽ���ߣ���BC=20cm����AM�ij�Ϊ$\frac{40}{3}$cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | d��1 | B�� | d��5 | C�� | 1��d��5 | D�� | 1��d��5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
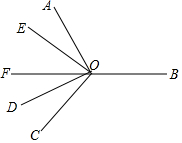 ��ͼ����ƽ���ڣ���AOB=��COB����AOD=��COE=90�㣬OFƽ�֡�DOE�������½��ۣ�
��ͼ����ƽ���ڣ���AOB=��COB����AOD=��COE=90�㣬OFƽ�֡�DOE�������½��ۣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | x��23 | B�� | 23��x��47 | C�� | 11��x��23 | D�� | x��47 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
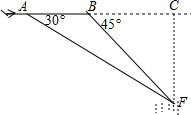 �������¼����ķ����������ҹ������ĸ߶����ӣ��ҹ�����Ѹ���ɳ��˽����ͷɻ�����غ��������Ѱ����ͼ����һ�ο�����Ѱ�У�ˮƽ���еķɻ��ڵ�A�����ǰ������ĵ�F�������Ʒɻ��к������壨��������Ϊ��ֹ������ʱ�ĸ���Ϊ30�㣬Ϊ�˱��ڹ۲죬�ɻ�������ǰ������800����B�㣬��ʱ��õ�F�㸩��Ϊ45�㣮������㵱�ɻ�����F������Ϸ���Cʱ����A��B��C��ͬһֱ���ϣ�����ֱ�߶�CFԼΪ�����ף�����������������ο���ֵ��$\sqrt{3}$��1.7��
�������¼����ķ����������ҹ������ĸ߶����ӣ��ҹ�����Ѹ���ɳ��˽����ͷɻ�����غ��������Ѱ����ͼ����һ�ο�����Ѱ�У�ˮƽ���еķɻ��ڵ�A�����ǰ������ĵ�F�������Ʒɻ��к������壨��������Ϊ��ֹ������ʱ�ĸ���Ϊ30�㣬Ϊ�˱��ڹ۲죬�ɻ�������ǰ������800����B�㣬��ʱ��õ�F�㸩��Ϊ45�㣮������㵱�ɻ�����F������Ϸ���Cʱ����A��B��C��ͬһֱ���ϣ�����ֱ�߶�CFԼΪ�����ף�����������������ο���ֵ��$\sqrt{3}$��1.7���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com