
分析 先将除法转化为乘法,然后利用乘法分配律进行解答,约分得到最简结果,将x的值代入计算即可求出值.
解答 解:($\frac{x+2}{{x}^{2}-2x}$-$\frac{x-1}{{x}^{2}-4x+4}$)÷$\frac{x-4}{{x}^{2}-2x}$,
=[$\frac{x+2}{x(x-2)}$-$\frac{x-1}{(x-2)^{2}}$]×$\frac{x(x-2)}{x-4}$
=$\frac{x+2}{x(x-2)}$×$\frac{x(x-2)}{x-4}$-$\frac{x-1}{(x-2)^{2}}$×$\frac{x(x-2)}{x-4}$
=$\frac{x+2}{x-4}$-$\frac{x(x-1)}{(x-2)(x-4)}$
=$\frac{(x+2)(x-2)-x(x-1)}{(x-2)(x-4)}$
=$\frac{1}{x-2}$.
当x=5时,原式=$\frac{1}{3}$.
点评 本题考查了分式的化简求值.化简求值,一般是先化简为最简分式或整式,再代入求值.化简时不能跨度太大,而缺少必要的步骤,代入求值的模式一般为“当…时,原式=…”.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:填空题
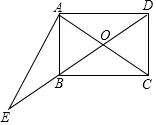 如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则$\frac{AO}{AE}$的值为$\frac{7}{24}$.
如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则$\frac{AO}{AE}$的值为$\frac{7}{24}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
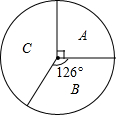 某校对1500名在校学生进行每周上网的情况调查,A为每天上网的学生,B为从不上网的学生,C为偶尔上网的学生,如扇形统计图所示.请根据图上信息,解答以下问题:
某校对1500名在校学生进行每周上网的情况调查,A为每天上网的学生,B为从不上网的学生,C为偶尔上网的学生,如扇形统计图所示.请根据图上信息,解答以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 应试者 | 测试成绩 | ||
| 创新能力 | 计算机能力 | 公关能力 | |
| 甲 | 72 | 50 | 88 |
| 乙 | 85 | 74 | 45 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
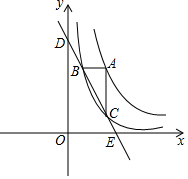 如图,点A在函数y=$\frac{4}{x}$(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=$\frac{1}{x}$图象于点B、C,直线BC与坐标轴的交点为D、E.当点A在函数y=$\frac{4}{x}$(x>0)图象上运动时,
如图,点A在函数y=$\frac{4}{x}$(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=$\frac{1}{x}$图象于点B、C,直线BC与坐标轴的交点为D、E.当点A在函数y=$\frac{4}{x}$(x>0)图象上运动时,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
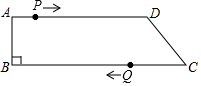 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=30cm.点P从点A出发,以1cm/s的速度向点D移动,点Q从点C出发,以3cm/s的速度向点B运动,点P和点Q分别从点A和点C同时出发,移动时间为ts.规定若其中一个动点先到达端点(终点)时,另一个动点也随之停止运动.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=30cm.点P从点A出发,以1cm/s的速度向点D移动,点Q从点C出发,以3cm/s的速度向点B运动,点P和点Q分别从点A和点C同时出发,移动时间为ts.规定若其中一个动点先到达端点(终点)时,另一个动点也随之停止运动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com