
【题目】![]() ,
,![]() ,
,![]() 为
为![]() 的角平分线.
的角平分线.
(1)如图1,若![]() ,则
,则![]() ______;若
______;若![]() ,则
,则![]() ______;猜想:
______;猜想:![]() 与
与![]() 的数量关系为______
的数量关系为______
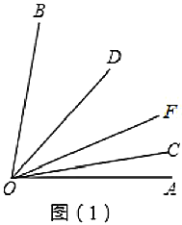
(2)当![]() 绕点
绕点![]() 按逆时针旋转至图2的位置时,(1)的数量关系是否仍然成立?请说明理由.
按逆时针旋转至图2的位置时,(1)的数量关系是否仍然成立?请说明理由.
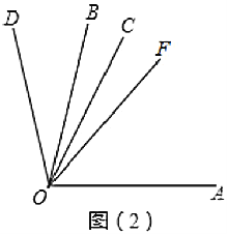
(3)如图3,在(2)的条件下,在![]() 中作射线
中作射线![]() ,使
,使![]() ,且
,且![]() ,直接写出
,直接写出![]() ______.
______.

【答案】(1)![]() ,
,![]() ,
,![]() ;(2)见解析;(3)16°
;(2)见解析;(3)16°
【解析】
(1)由已知求出∠DOF=30°,由角平分线得出∠AOF=∠DOF=30°,得出∠AOD=60°,求出∠BOD=∠AOB-∠AOD=20°;若∠COF=m°,则∠DOF=40°-m°,由角平分线得出∠AOF=∠DOF=40°-m°,得出∠AOD=80°-2m°,得出∠BOD=∠AOB-∠AOD=2m°,即可得出结论;
(2)设![]() ,则
,则![]() ,利用角平分线的性质即可得出
,利用角平分线的性质即可得出![]() ,(1)的数量关系依然成立;
,(1)的数量关系依然成立;
(3)设![]() ,则
,则![]() ,得出
,得出![]() ,由角平分线得出
,由角平分线得出![]() ,由∠AOB=80°得出方程,解方程求出
,由∠AOB=80°得出方程,解方程求出![]() ,即可得出结果.
,即可得出结果.
(1)∵![]() ,
,![]()
∴∠FOD=∠COD-∠COF=40°-10°=30°
∵![]() 为
为![]() 的角平分线
的角平分线
∴∠AOD=2∠FOD=60°
∵![]() ,
,
∴∠BOD=∠AOB-∠AOD=80°-60°=20°
同理可得,∠BOD=![]() ,
,
∵∠COD=40°,∠COF=10°,
∴∠DOF=30°,
∵OF为∠AOD的角平分线.
∴∠AOF=∠DOF=30°,
∴∠AOD=60°,
∴∠BOD=∠AOB-∠AOD=20°;
∵∠COD=40°,∠COF=m°,
∴∠DOF=40°-m°,
∵OF为∠AOD的角平分线.
∴∠AOF=∠DOF=40°-m°,
∴∠AOD=80°-2m°,
∴∠BOD=∠AOB-∠AOD=2m°,
∴∠BOD=2∠COF;
通过上述两种求法,可得![]() .
.
(2)∵![]() ,设
,设![]() ,则
,则![]() .
.
∵![]() 为
为![]() 的角平分线,
的角平分线,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() .(1)的数量关系依然成立.
.(1)的数量关系依然成立.
(3)设![]() ,则
,则![]() ,
,
∴![]() ,
,
∵![]() 为
为![]() 的平分线,
的平分线,
∴![]()
∵![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]()


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
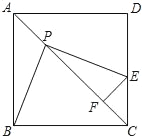
【题目】已知边长为1的正方形ABCD中, P是对角线AC上的一个动点(与点A、C不重合),过点P作PE⊥PB ,PE交射线DC于点E,过点E作EF⊥AC,垂足为点F.
(1)当点E落在线段CD上时(如图),
①求证:PB=PE;
②在点P的运动过程中,PF的长度是否发生变化?若不变,试求出这个不变的值,若变化,试说明理由;
(2)当点E落在线段DC的延长线上时,在备用图上画出符合要求的大致图形,并判断上述(1)中的结论是否仍然成立(只需写出结论,不需要证明);
(3)在点P的运动过程中,△PEC能否为等腰三角形?如果能,试求出AP的长,如果不能,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由相同的花盆按一定的规律组成的形如正多边形的图案,其中第1个图形共有6个花盆,第2个图形一共有12个花盆,第3个图形一共有20个花盆,…,则第10个图形中花盆的个数为( )

A. 110B. 120C. 132D. 140
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图2是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )

A. 第24天的销售量为200件 B. 第10天销售一件产品的利润是15元
C. 第12天与第30天这两天的日销售利润相等 D. 第30天的日销售利润是750元
查看答案和解析>>
科目:初中数学 来源: 题型:
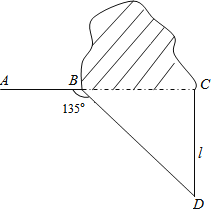
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(![]() ≈1.414,精确到1米)
≈1.414,精确到1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的A、B两点所表示的数分别为a、b,a+b<0,ab<0.

(1)原点O的位置在
A.点A的右边
B.点B的左边
C.点A与点B之间 ,且靠近点A
D.点A与点B之间 ,且靠近点B
(2)若a-b=2,
①利用数轴比较大小,a 1,b -1;(填“>”、“<”或“=”).
②化简:|a-1|+|b+1|.
查看答案和解析>>
科目:初中数学 来源: 题型:
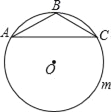
【题目】如图,△ABC中,AB=BC,∠ABC=120°,AC=2![]() ,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
A. y=![]() x+4 B. y=
x+4 B. y=![]() x+4 C. y=
x+4 C. y=![]() x2+4 D. y=
x2+4 D. y=![]() x2+4
x2+4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com