
 如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q,与x轴交于点T.
如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q,与x轴交于点T.分析 (1)通过解方程x2-4x得A(4,0),则利用对称性得到抛物线的对称轴;直线x=2交x轴于B点,如图,求出B(2,0),Q,2,2+m),T(-m,0),接着判断△BQT为等腰直角三角形,则可判断直线PQ与x轴所夹锐角的度数为45°;
(2)作AE⊥PQ于E,OF⊥PQ于F,如图,求出$\frac{OF}{AE}$=$\frac{1}{3}$,通过三角形面积公式可得到△POQ与△PAQ的面积比;
(3)利用线段的中点坐标公式得到P($\frac{2-m}{2}$,$\frac{2+m}{2}$),然后把P点坐标代入抛物线解析式得到关于m的方程,再通过解方程可判断是否存在实数m,使得点P为线段QT的中点.
解答 解:(1)当y=0时,x2-4x=0,解得x1=0,x2=4,则A(4,0),
所以抛物线的对称轴为直线x=2;
直线x=2交x轴于B点,如图,则B(2,0),
当x=2时,y=2+m,则Q(2,2+m),
当y=0时,x+m=0,解得x=-m,则T(-m,0),
因为BT=|2+m|,QB=|2+m|,
所以BT=QB,
所以△BQT为等腰直角三角形,
所以∠QTB=45°,即直线PQ与x轴所夹锐角的度数为45°;
故答案为直线x=2,45°;
(2)作AE⊥PQ于E,OF⊥PQ于F,如图,
∵OF∥AE,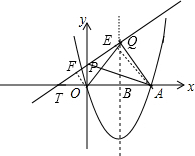
∴$\frac{OF}{AE}$=$\frac{OT}{AT}$,
当m=2时,T(-2,0),
∴$\frac{OF}{AE}$=$\frac{2}{2+4}$=$\frac{1}{3}$,
∴△POQ与△PAQ的面积比=$\frac{1}{3}$;
(3)存在.
∵T(-m,0),Q(2,2+m),
而P点为TQ的中点,
∴P($\frac{2-m}{2}$,$\frac{2+m}{2}$),
把P($\frac{2-m}{2}$,$\frac{2+m}{2}$)代入y=x2-4x得($\frac{2-m}{2}$)2-4•$\frac{2-m}{2}$=$\frac{2+m}{2}$,
整理得m2+2m-16=0,解得m1=-1+$\sqrt{17}$,m2=-1-$\sqrt{17}$,
即m的值为-1+$\sqrt{17}$或-1-$\sqrt{17}$时,使得点P为线段QT的中点.
点评 本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.解决(2)小题的关键求出点O和点P到直线PQ的比,解决(3)小题的关键是用m表示出P点坐标.


科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,给出如下定义:形如y=(x-m)(x-m+1)与y=(x-m)(x-m-1)的两个二次函数的图象叫做兄弟抛物线.
在平面直角坐标系中,给出如下定义:形如y=(x-m)(x-m+1)与y=(x-m)(x-m-1)的两个二次函数的图象叫做兄弟抛物线.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
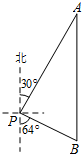 如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处.海轮沿正南方向航行一段时间后,到达位于灯塔P的南偏东64°方向上的B处.求海轮所在的B处与灯塔P的距离.(结果精确到0.1海里)(参考数据:sin64°=0.90,cos64°=0.44,tan64°=2.05)
如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处.海轮沿正南方向航行一段时间后,到达位于灯塔P的南偏东64°方向上的B处.求海轮所在的B处与灯塔P的距离.(结果精确到0.1海里)(参考数据:sin64°=0.90,cos64°=0.44,tan64°=2.05)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com