
分析 首先根据任意三个相邻数之和都是35,推出a1=a4,a2=a5,a3=a6,总结规律为a1=a3n+1,a2=a3n+2,a3=a3n,即可推出a20=a2=15,a99=a3=3-x=2x,求出a3=2,即可推出a1=18,由a2014=a671×3+1,推出a2014=a1=18.
解答 解:∵任意三个相邻数之和都是35,
∴a1+a2+a3=a2+a3+a4=35,a2+a3+a4=a3+a4+a5=35,a3+a4+a5=a4+a5+a6=35,
∴a1=a4,a2=a5,a3=a6,∴a1=a3n+1,a2=a3n+2,a3=a3n,∵20=3×6+2,a20=15,
∴a20=a2=15;
∵99=3×33,
∴a99=a3,
∵a3=2x,a99=3-x,
∴3-x=2x,
∴x=1,
∴a3=2,∵a1+a2+a3=35,
∴a1=35-15-2=18,
∵2014=671×3+1,
∴a2014=a1=18.
故答案为:18.
点评 本题主要考查通过分析题意总结规律,关键在于通过已知分析出a1=a3n+1,a2=a3n+2,a3=a3n,然后根据规律推出a20=a2,a99=a3,a2013=a3,然后根据规律解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
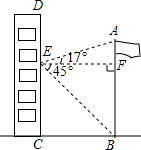 如图,在某次数学活动课中,小明为了测量校园内旗杆AB的高度,站在教学楼CD上的E处测得旗杆底端B的仰角∠BEF的度数为45°,测得旗杆顶端A的仰角∠AEF的度数为17°,旗杆底部B处与教学楼底部C处的水平距离BC为9m,求旗杆的高度(结果精确到0.1m).
如图,在某次数学活动课中,小明为了测量校园内旗杆AB的高度,站在教学楼CD上的E处测得旗杆底端B的仰角∠BEF的度数为45°,测得旗杆顶端A的仰角∠AEF的度数为17°,旗杆底部B处与教学楼底部C处的水平距离BC为9m,求旗杆的高度(结果精确到0.1m).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
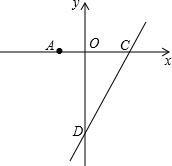 如图,点A的坐标为(-1,0),点B在直线y=2x-4上运动.
如图,点A的坐标为(-1,0),点B在直线y=2x-4上运动.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
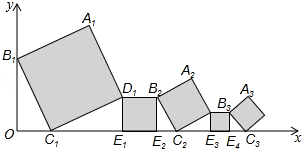 已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上且坐标是(0,2),点C1、E1、E2、C2、E3、E4、C3在x轴上,C1的坐标是(1,0).B1C1∥B2C2∥B3C3,以此继续下去,则点A4到x轴的距离是$\frac{3}{8}$.
已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上且坐标是(0,2),点C1、E1、E2、C2、E3、E4、C3在x轴上,C1的坐标是(1,0).B1C1∥B2C2∥B3C3,以此继续下去,则点A4到x轴的距离是$\frac{3}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
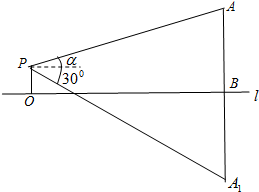 在湖心有一座塔,小明想知道这座塔的高度,于是他在岸边架起了测角仪.他测量得数据如下(如图示):测角仪位置(P)距水平面(l)的距离为1.5米(即OP),测得塔顶A的仰角为α(其中tanα=$\frac{1}{3}$),测得塔顶在水中倒影A1(即AB=A1B)的俯角为300.那么这座塔的高度AB=3+$\frac{3\sqrt{3}}{2}$.(结果保留根号)
在湖心有一座塔,小明想知道这座塔的高度,于是他在岸边架起了测角仪.他测量得数据如下(如图示):测角仪位置(P)距水平面(l)的距离为1.5米(即OP),测得塔顶A的仰角为α(其中tanα=$\frac{1}{3}$),测得塔顶在水中倒影A1(即AB=A1B)的俯角为300.那么这座塔的高度AB=3+$\frac{3\sqrt{3}}{2}$.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
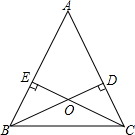 如图,锐角△ABC中AB=c,AC=b,BC=a且有b2-c2=ac-ab.
如图,锐角△ABC中AB=c,AC=b,BC=a且有b2-c2=ac-ab.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com